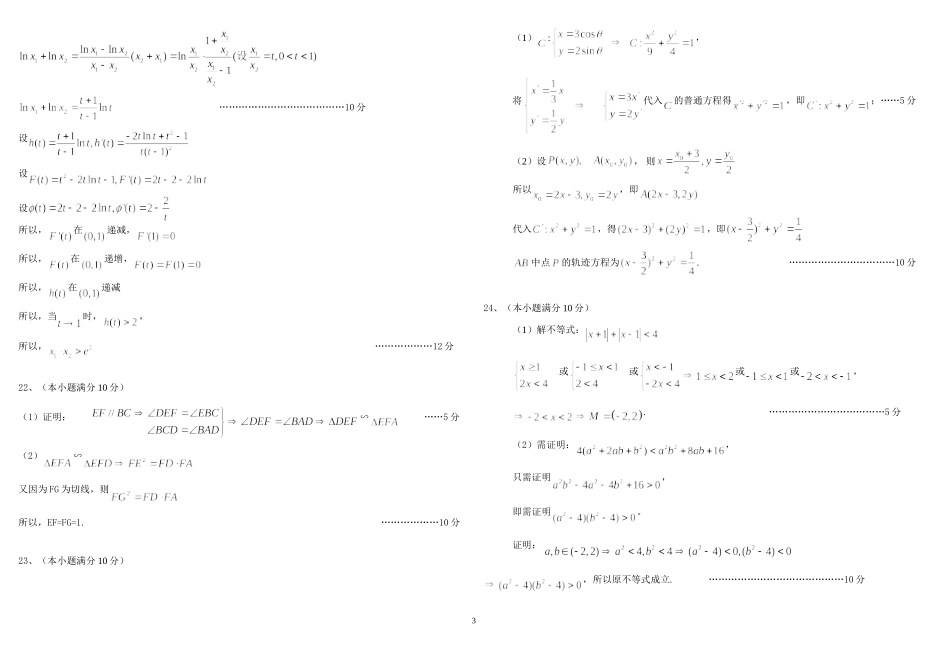
理科数学答案一、选择题:题号123456789101112答案BDCABABDCBAC二、填空题:13、5514、15、16、①②④三、解答题:17、(本小题满分12分)(1),由正弦定理得,………………………………4分.……………………………6分(2),……………………………8分又,所以,当且仅当取等号.…………………………10分,为正三角形时,.……………………………12分18、(本小题满分12分)(1)的频率为的频率为S统计意义:酒精浓度的平均数为……4分(2)70~90共有人的可能值为……………8分所以,的分布列为:012……………10分记“吴、李两位先生至少有1人被抽中”为事件A……………12分19、(本小题满分12分)(1)证明:连接BM,则AM=BM=,所以又因为面ADM平面ABCM,所以,(2)建立如图所示的空间直角作标系1由(1)可知,平面ADM的法向量设平面ABCM的法向量,所以,二面角DAME的余弦值为55得,,即:E为DB的中点。20、(本小题满分12分)(1)在线段的垂直平分线上,所以;得,又,得的轨迹是以为焦点,长轴长为4的椭圆..…………………………………………………4分(2)当AB的斜率存不存在或为零时,|AB|=4,|OC|=1,S=2;|AB|=2,|OC|=2,S=2当AB的斜率存存在且不为零时,与关于原点对称,设,在的垂直平分线上,.,,同理可得,…………………6分…………………………8分,当且仅当时取等号,所以,………………………………………………………………………………11分当时.………………12分21、(本小题满分10分)(1)切线方程为:…………………………………………3分(2)①当,所以,在递增,②当时,,所以,在递减,③当,递增,递减………7分(3)设所以,在递增,递减,所以,2…………………………………10分设设设所以,在递减,所以,在递增,所以,在递减所以,当时,,所以,………………12分22、(本小题满分10分)(1)证明:∽……5分(2)∽又因为FG为切线,则所以,EF=FG=1.………………10分23、(本小题满分10分)(1):,将代入的普通方程得,即;……5分(2)设,则所以,即代入,得,即中点的轨迹方程为.……………………………10分24、(本小题满分10分)(1)解不等式:或或或或,.………………………………5分(2)需证明:,只需证明,即需证明。证明:,所以原不等式成立.……………………………………10分3