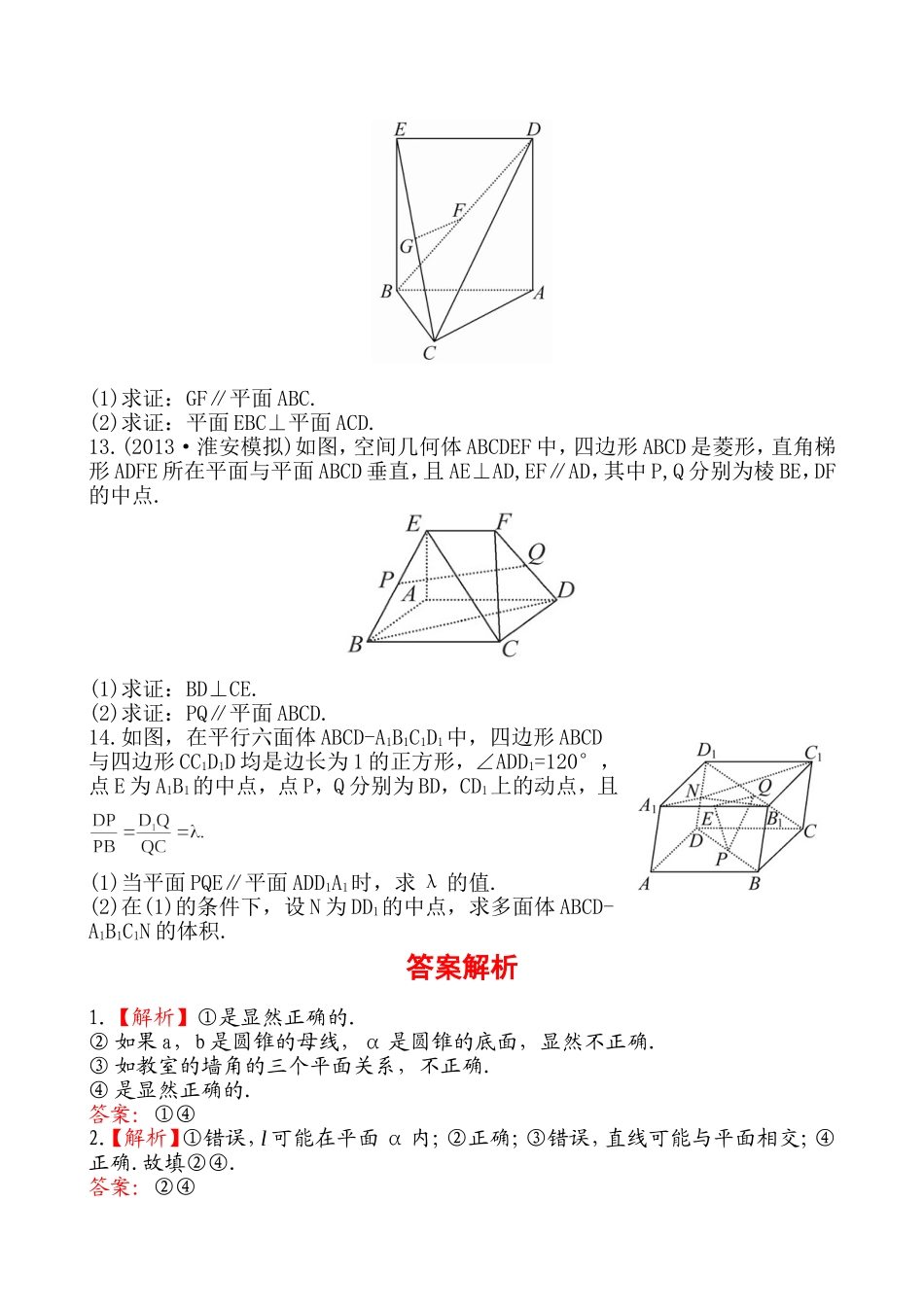
温馨提示:此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。关闭Word文档返回原板块。课时提升作业(四十七)一、填空题1.(2013·宿迁模拟)已知a,b是直线,α,β,γ是平面,给出下列命题:①若α∥β,a⊂α,则a∥β;②若a,b与α所成角相等,则a∥b;③若α⊥β,β⊥γ,则α∥γ;④若a⊥α,a⊥β,则α∥β.其中正确的命题的序号是_______.2.设α,β,γ是三个不重合的平面,l是直线,给出下列四个命题:①若α⊥β,l⊥β,则l∥α;②若l⊥α,l∥β,则α⊥β;③若l上有两点到α的距离相等,则l∥α;④若α⊥β,α∥γ,则γ⊥β.其中正确命题的序号是_________.3.如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,当点M满足________时,平面MBD⊥平面PCD(只要填写一个你认为是正确的条件即可).4.设X,Y,Z是空间不同的直线或平面,对下列四种情形,使“X⊥Z且Y⊥Z⇒X∥Y”为真命题的是________(填序号).①X,Y,Z是直线;②X,Y是直线,Z是平面;③Z是直线,X,Y是平面;④X,Y,Z是平面.5.如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,给出下列结论:①PB⊥AD;②平面PAB⊥平面PBC;③直线BC∥平面PAE;④直线PD与平面ABC所成的角为45°.则所有正确结论为_________(填序号).6.已知三个不同的平面α,β,γ,a,b,c分别为平面α,β,γ内的直线,若β⊥γ且α与γ相交但不垂直,则下列命题为真命题的个数为________.①任意b⊂β,b⊥γ;②任意b⊂β,b∥γ;③存在a⊂α,a⊥γ;④存在a⊂α,a∥γ;⑤任意c⊂γ,c∥α;⑥存在c⊂γ,c⊥β.7.(2013·南通模拟)如图所示的“双塔”形立体建筑,已知P-ABD和Q-CBD是两个高相等的正三棱锥,四点A,B,C,D在同一平面内,要使塔尖P,Q之间的距离为50m,则底边AB的长为_______m.8.点P在正方体ABCD-A1B1C1D1的面对角线BC1上运动,则下列三个命题中正确的个数是_________.①三棱锥A-D1PC的体积不变;②A1P∥平面ACD1;③DP⊥BC1.9.如图,在直角梯形ABCD中,BC⊥DC,AE⊥DC,M,N分别是AD,BE的中点,将三角形ADE沿AE折起.下列说法正确的是_______.(填上所有正确的序号)①不论D折至何位置(不在平面ABC内)都有MN∥平面DEC;②不论D折至何位置都有MN⊥AE;③不论D折至何位置(不在平面ABC内)都有MN∥AB.10.(能力挑战题)正四棱锥S-ABCD的底面边长为2,高为2,E是边BC的中点,动点P在表面上运动,并且总保持PE⊥AC,则动点P的轨迹的周长为______.二、解答题11.(2013·南京模拟)如图,已知斜三棱柱ABC-A1B1C1中,AB=AC,D为BC的中点.(1)若平面ABC⊥平面BCC1B1,求证:AD⊥DC1.(2)求证:A1B∥平面ADC1.12.如图,△ABC中,AC⊥BC,四边形ABED是正方形,平面ABED⊥平面ABC,若G,F分别是EC,BD的中点.(1)求证:GF∥平面ABC.(2)求证:平面EBC⊥平面ACD.13.(2013·淮安模拟)如图,空间几何体ABCDEF中,四边形ABCD是菱形,直角梯形ADFE所在平面与平面ABCD垂直,且AE⊥AD,EF∥AD,其中P,Q分别为棱BE,DF的中点.(1)求证:BD⊥CE.(2)求证:PQ∥平面ABCD.14.如图,在平行六面体ABCD-A1B1C1D1中,四边形ABCD与四边形CC1D1D均是边长为1的正方形,∠ADD1=120°,点E为A1B1的中点,点P,Q分别为BD,CD1上的动点,且(1)当平面PQE∥平面ADD1A1时,求λ的值.(2)在(1)的条件下,设N为DD1的中点,求多面体ABCD-A1B1C1N的体积.答案解析1.【解析】①是显然正确的.②如果a,b是圆锥的母线,α是圆锥的底面,显然不正确.③如教室的墙角的三个平面关系,不正确.④是显然正确的.答案:①④2.【解析】①错误,l可能在平面α内;②正确;③错误,直线可能与平面相交;④正确.故填②④.答案:②④3.【解析】由定理可知,BD⊥PC,∴当DM⊥PC(或BM⊥PC)时,即有PC⊥平面MBD,而PC⊂平面PCD,∴平面MBD⊥平面PCD.故填DM⊥PC(或BM⊥PC等).答案:DM⊥PC(或BM⊥PC等)4.【解析】由垂直于同一个平面的两条直线平行,垂直于同一条直线的两个平面平行,可知②③正确.答案:②③5.【解析】 AD与PB在平面ABC内的射影AB不垂直,∴①不成立;又平面PAB⊥平面PAE,∴平面PAB⊥平面PBC也不成立,即②不成立...