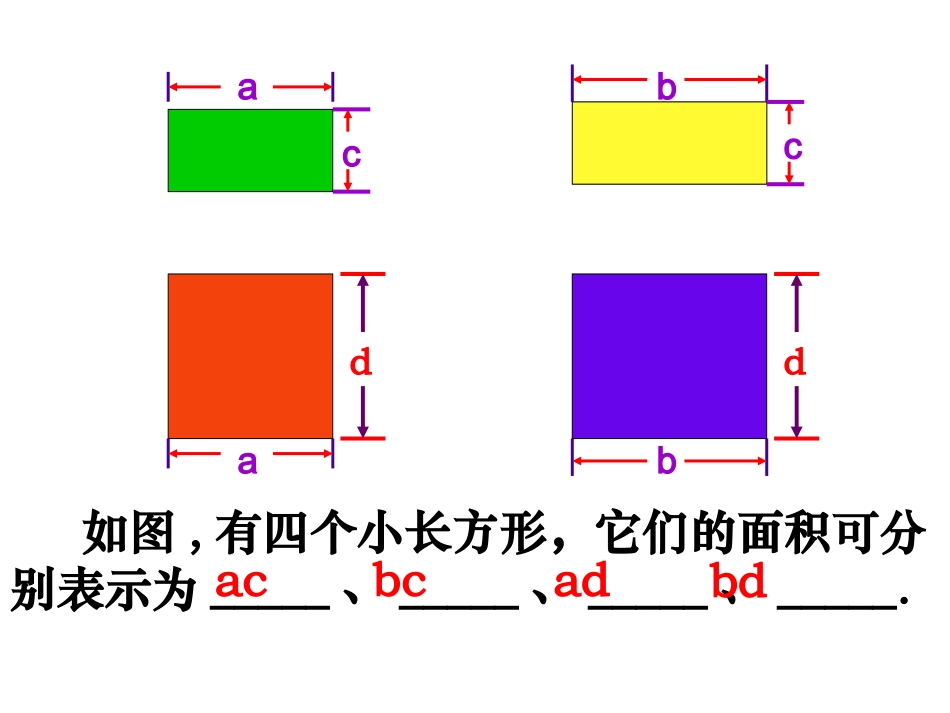
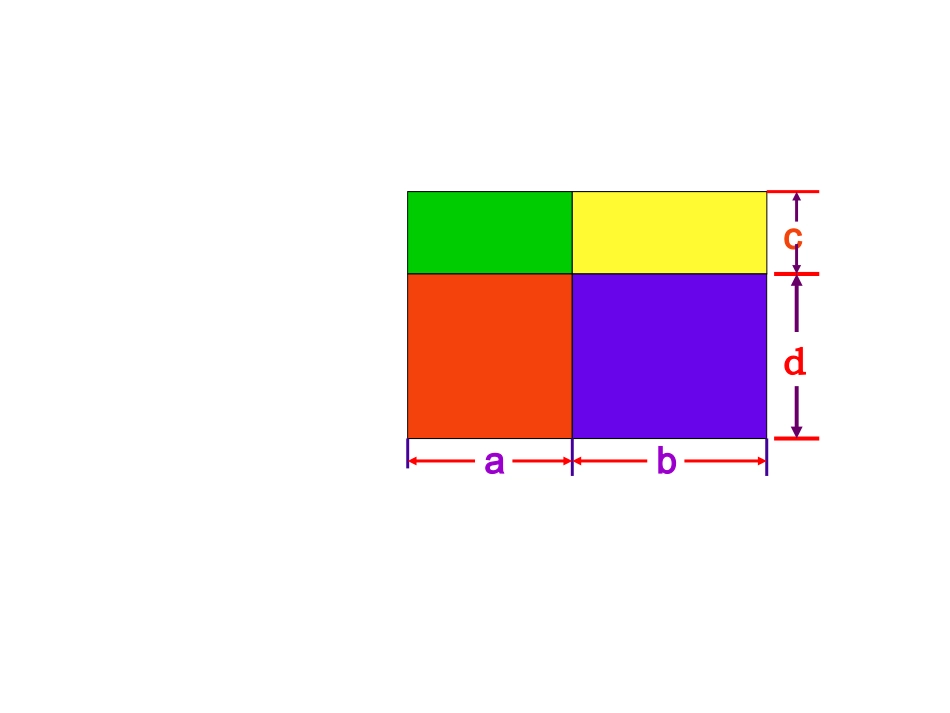
多项式乘多项式如图,有四个小长方形,它们的面积可分别表示为_____、_____、_____、_____.dacadbcdababccbddabcdabc如果把它看成由四个小长方形组成,那么它的面积可表示为____________.ac+bc+ad+bd(a+b)(c+d)ac+bc+ad+bd如果把它看成一个大长方形,那么它的边长为_____、_____,面积可表示为_________.c+d(a+b)(c+d)a+b(a+b)(c+d)ad+bcac+根据单项式乘多项式法则ac+bc+ad+bd(a+b)(c+d)bd+a(c+d)b(c+d)+根据乘法的分配律(a+b)(c+d)ad+bcac+ac+bc+ad+bd(a+b)(c+d)bd+这个运算过程,也可以表示为如何进行多项式乘多项式的运算?多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.多项式乘多项式的法则(a+b)(c+d)ac+bc+ad+bd=例1计算下列各式(1)(3x+1)(x-2)(2)(2x-5y)(3x-y)(3)13()(32)3xx注意:多项式与多项式相乘的结果中,要合并同类项.解(1)原式=3x•x+3x•(-2)+1•x+1•(-2)=3x2-6x+x-2=3x2-5x-21.填空:(1)(2x+y)(x-y)=__________.(2)(m+2n)(m-2n)=________.(3)(2m+5)(2m-3)=_____________.(4)(1-x)(0.6-x)=____________.(5)(x+2y)(x+8y)=____________.2.计算:⑴2(x+1)(x-1)⑵(a+b)(a-b)-a(a-b)2x2-xy-y2m2-4n24m2+10m-15x2-1.6x+0.6x2+10xy+16y2例2:计算:(1)n(n+1)(n+2)解:原式=(n2+n)(n+2)=n3+2n2+n2+2n=n3+3n2+2n想一想(2)(x+4)2-(8x-16)解:原式=(x+4)(x+4)-(8x-16)=x2+4x+4x+16-8x+16=x2+32练一练计算3.(X-3)2-(X+3)(X-1)1.n(n+2)(2n+1)2.(y+1)(y-1)(y2+1)想一想例3:计算:(1)(a+4)(a+3)(2)(x+2)(x-3)(3)(x-2)(x-3)解:(1)原式=a2+3a+4a+12=a2+7a+12(2)原式=x2-3x+2x-6=x2-x-6(3)原式=x2-3x-2x+6=x2-5x+6=a2+7a+12=x2-x-6=x2-5x+6一般地,(x+a)(x+b)=x2+ax+bx+ab=x2+(a+b)x+ab口答:(1)(x+1)(x+2)(2)(x+1)(x-2)(3)(x-1)(x-2)(4)(x+2)(x-1)1.解方程:(1)(3x-2)(2x-3)=(6x+5)(x-1)-1(2)(x-2)(x+3)-(x+2)(x-5)=62.先化简,再求值.5x2-(2x+1)(3x-2)+(x+3)(x-3),其中x=21想一想如果(x-3)(3x+5)=ax2+bx+c,求a,b,c的值。例4想一想解:(x-3)(3x+5)=3x2+5x-9x-15=3x2-4x-15=ax2+bx+c所以a=3,b=-4,c=-15思考题如果(x+a)(x+b)=x2+3x-4,求(a+b)-ab的值。想一想解:(x+a)(x+b)=x2+ax+bx+ab=x2+(a+b)x+ab=x2+3x-4所以a+b=3,ab=-4(a+b)-ab=3-(-4)=7小结与回顾小结与回顾