《面面垂直的判定与性质》VIP免费

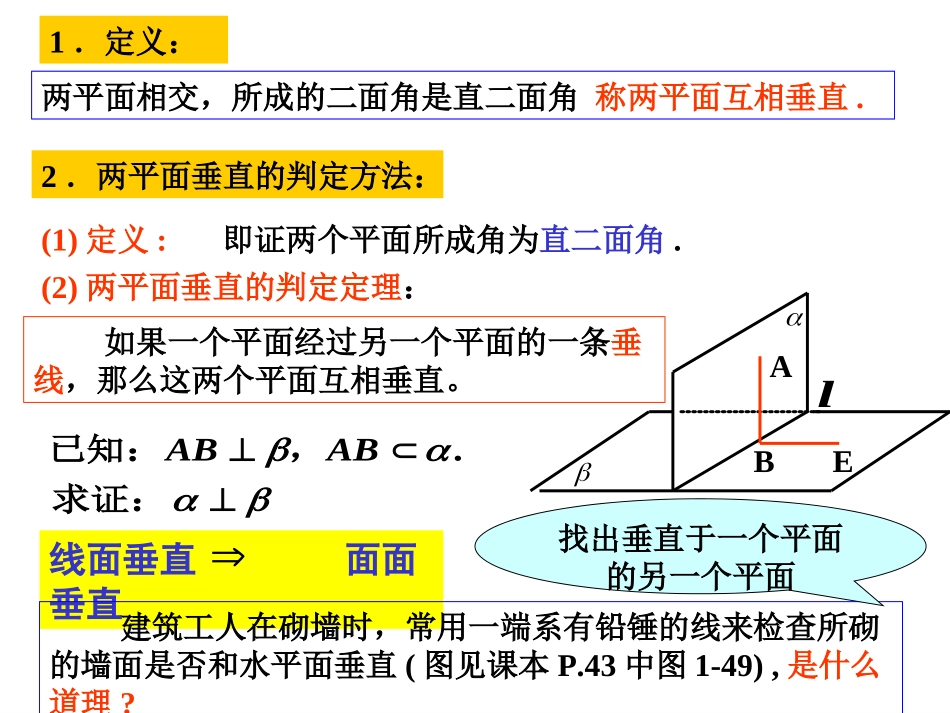
两个平面的位置关系----两平面垂直复习：一条直线可以把一个平面分成多少部分？每一部分都叫做半平面半平面2部分从一条直线出发的两个半平面所组成的的图形叫二面角二面角.二面角的棱棱、二面角的面面，记作：a在棱上取点O，分别在两个半平面上作垂直于a的的直线OA、OB，把叫二面角的平面角。AOB此时二面角为若,900AOB直二面角直二面角两平面相交，所成的二面角是直二面角称两平面互相垂直.1．定义：2．两平面垂直的判定方法：如果一个平面经过另一个平面的一条垂线，那么这两个平面互相垂直。ElAB求证：，已知：.ABAB线面垂直面面垂直(1)定义:即证两个平面所成角为直二面角.(2)两平面垂直的判定定理：建筑工人在砌墙时，常用一端系有铅锤的线来检查所砌的墙面是否和水平面垂直(图见课本P.43中图1-49),是什么道理?找出垂直于一个平面的另一个平面应用：如何检测所砌的墙面和地面是否垂直？三．应用：。平面证：平面是圆周上任意一点，求，所在平面垂直于圆的直径，是圆：例VBCVCACOVAOAB1OABCV。平面？中找一条线或在平面平面？中找一条线在平面VCAVBCVBCVCA？有几对相互垂直的平面有几个直角三角形？中，－思考：在四面体ABCV4个3对注：用判定定理证面面垂直08-10-08如果一个平面经过另一个平面的一条垂线，则这两个平面互相垂直如果一个平面经过另一个平面的一条垂线，则这两个平面互相垂直PABC PA⊥面ABC∴面PAC⊥面ABC∴面PAB⊥面ABC BC⊥面PAC∴面PBC⊥面PAC∴面ABC⊥面PAC判定定理：如果一个平面经过另一个平面的一条垂线，那么这两个平面相互垂直.例例1:1:在正方体在正方体ABCD-A’B’C’D’ABCD-A’B’C’D’中中,,求证求证::平面平面A’C’CA⊥A’C’CA⊥平面平面B’D’DB.B’D’DB.ABCDA1B1C1D1练习1在正方体ABCD—A1B1C1D1中,(1)求证：平面A1C⊥平面B1DACDA1C1D1EFＢB1(2)若E、F分别是AB、BC的中点，求证：平面A1C1FE⊥平面B1D(3)若G是BB1的中点求证：平面A1C1G⊥平面B1DGGGG3.两个平面垂直的性质两个平面垂直的性质定理如果两个平面垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面。E已知：.ABCDABCD，，，求证：ABDCβαAB αβ⊥，∴ABBE⊥．又 ABCD⊥，∴ABβ⊥．证明：在平面β内引直线BECD⊥，则∠ABE是二面角α-CD-β的平面角．面面垂直线面垂直aaaPP求证：（如图）已知：.,,,例2求证：如果两个平面互相垂直，那么经过第一个平面内的一点垂直于第二个平面的直线，在第一个平面内。abβαcPβαabcP证明(同一法)：设α∩β＝c，过点P在平面α内作直线bc⊥，根据上面的定理有bβ⊥．因为经过一点只能有一条直线与平面β垂直，所以直线a应与直线b重合．性质推论练习2已知α∩β＝l,α⊥γ,β⊥γ.求证l⊥γ.αβγlαβγlPEFαβγlQPDEACDEBCDEBClABABl，求证：，，，，，＝，、如图：例3αβlABCDE。平面求证：平面。＝，＝＝所在平面外一点，是：已知例ABCPBCBACPCPBPAABCP0904ABCP.OPOBC，连中点证明：取O,OCOBOA则BCPO2222OCPOOAPO由2PAOAPO得ABCPO面08-10-08四面体ABCD中，面ADC⊥面BCD，面ABD⊥面BCD，设DE是BC边上的高，求证：平面ADE⊥面ABCABCED面ADC⊥面BCD面ABD⊥面BCDAD⊥面BCDADBC⊥DEBC⊥BC⊥面ADE面ABC⊥面ADE①②③④线面垂直面面垂直线线垂直①②③④08-10-08课堂练习课堂练习空间四面体ABCD中，若AB=BC，AD=CD，E为AC的中点，则有（）ABCED(A)平面ABD⊥面BCD(B)平面BCD⊥面ABC(C)平面ACD⊥面ABC(D)平面ACD⊥面BDE08-10-08如图，ABCD是正方形，PA⊥面ABCD，连接PB,PC,PD,AC,BD,问图中有几对互相垂直的平面？ABDPC面PAC⊥面ABCD面PAB⊥面ABCD面PAD⊥面ABCD面PAD⊥面PAB面PAD⊥面PCD面PBC⊥面PAB面PBD⊥面PAC补充1.如图P为ΔABC所在平面外一点，PA⊥平面ABC，∠ABC＝90°，AEPB⊥于E，AFPC⊥于F.求证：PABCEF⑴平面PAB⊥平面PBC；⑵平面AEF⊥平面PBC；⑶平面AEF⊥平面PAC。证明面面垂直的方法：1．定义：二面角为直二面角2．判定定理：aa...