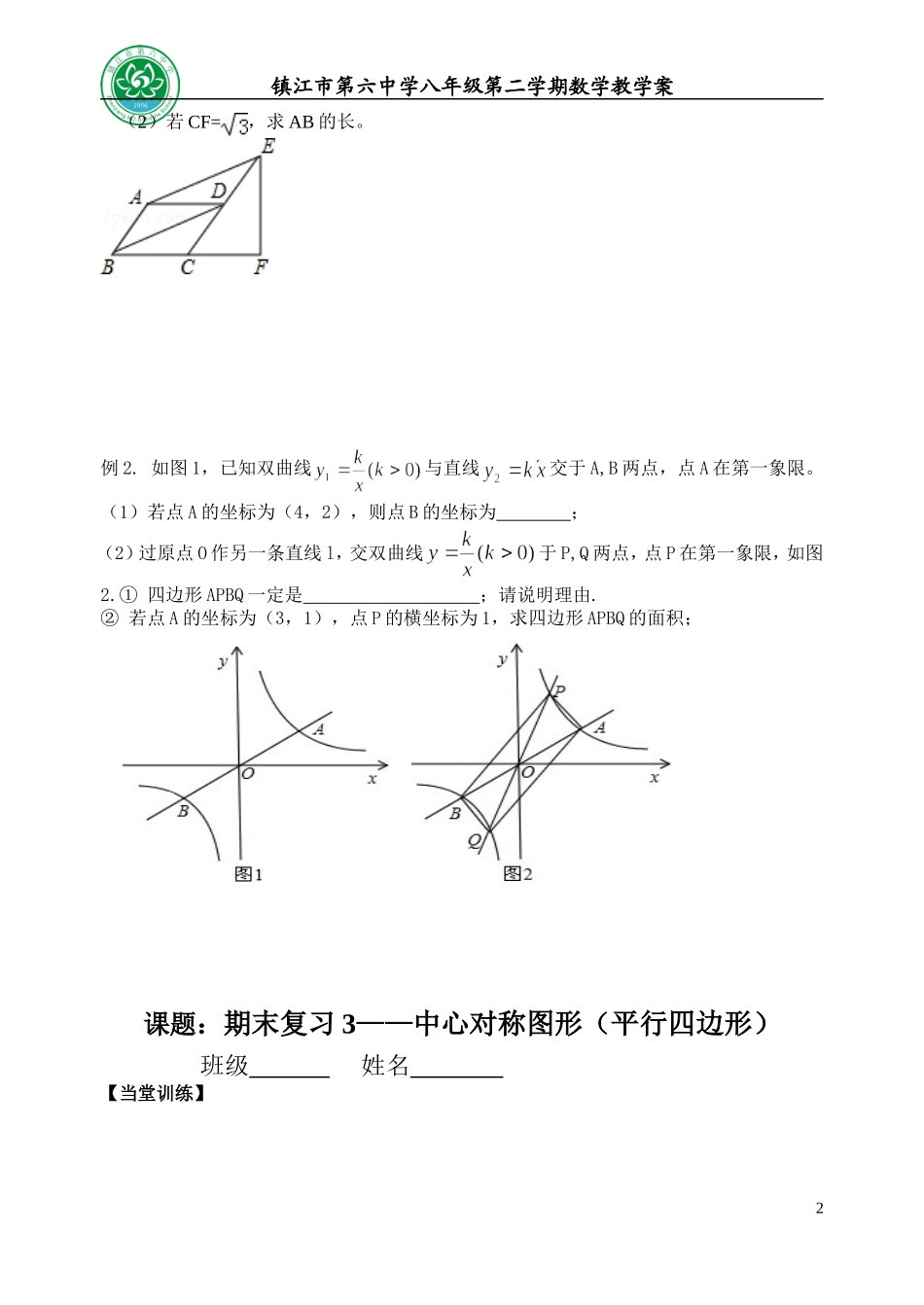
镇江市第六中学八年级第二学期数学教学案课题:期末复习3——中心对称图形(平行四边形)主备:陈丽课型:复习审核:八年级数学组班级姓名【学习目标】1、认识图形的旋转及性质,会根据要求画旋转图形。2、认识中心对称图形及其性质。3、理解并掌握中心对称图形(平行四边形)的性质、判定及其应用。【学习重难点】灵活运用中心对称图形(平行四边形)的性质、判定及其应用。【知识要点】1、图形旋转的性质:旋转前后的图形,对应点到,每一对对应点与。2、中心对称图形:把一个平面图形绕某一点旋转,如果旋转后的图形能够和原来的图形互相,那么这个图形叫做中心对称图形。3、平行四边形的性质:(1)平行四边形是对称图形,(2平行四边形对边______;对角_________;邻角________;对角线______。4、平行四边形的判定:(1)两组对边分别的四边形是平行四边形;(2)两组对边分别的四边形是平行四边形。(3)一组对边的四边形是平行四边形;(4)两条的四边形是平行四边形;【课前准备】EDCAB2.在□ABCD中,对角线相交于点O.(1)若∠A-∠B=70°,则∠C=___,∠D=_________.(2)若两邻边之比为2∶3,周长为20cm,则这个平行四边形的两邻边分别为__________.(3)若AC=10,BD=18,AD=12,则△BOC的周长是___________.3.若平行四边形的一边长为12,则其对角线的值可能是()A、8和14B、10和14C、18和20D、10和344.如图,□ABCD中,E、F分别是BC和AD边上的点,且BE=DF,请说明AE与CF的关系,并说明理由。【例题精选】例1.如图□ABCD中,∠ABC=60°,E、F分别在CD和BC的延长线上,AEBD∥,EFBC⊥,(1)求证:点D是EC的中点;1FEDCBA1.如图,在△ABC中,∠ACB=90°,∠A=35°,将△ABC绕点C旋转到△DEC处,使点B恰好落在边DE上,则点A旋转到了________,旋转中心是__________,旋转角度数为_________°镇江市第六中学八年级第二学期数学教学案(2)若CF=,求AB的长。例2.如图1,已知双曲线与直线交于A,B两点,点A在第一象限。(1)若点A的坐标为(4,2),则点B的坐标为;(2)过原点O作另一条直线l,交双曲线于P,Q两点,点P在第一象限,如图2.①四边形APBQ一定是;请说明理由.②若点A的坐标为(3,1),点P的横坐标为1,求四边形APBQ的面积;课题:期末复习3——中心对称图形(平行四边形)班级姓名【当堂训练】2镇江市第六中学八年级第二学期数学教学案1、□ABCD中,若∠A+∠C=130o,则∠D的度数是.2、如图,在平面直角坐标系中,△ABC与△A1B1C1关于点E成中心对称.(1)画出对称中心点E,并写出点E、A、C的坐标;(2)画出△ABC关于坐标原点对称的△A2B2C2.3、如图,在□ABCD中,点E、F在AC上,且AF=CE,点G、H分别在AB、CD上,且AG=CH,AC与GH相交于点O,试说明:(1)EG∥FH,(2)GH、EF互相平分。4、如图,在等边三角形ABC中,BC=6cm,射线AGBC∥点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,如果E、F同时出发,当t为多少时,以A、E、F、C为顶点的四边形是平行四边形?5、已知平行四边形的三个顶点A(2,0)、B(2,3)、C(-1,1),求第四个顶点D的坐标。【课后巩固】1、下列图形中,是中心对称图形的是()3OHGFADCBE镇江市第六中学八年级第二学期数学教学案2、如图,在□ABCD中,DB=DC,∠C=70°,AE⊥BD于E,则∠DAE等于()A.20°B.25°C.30°D.35°第2题第3题3、如图,□ABCD中,BC∶AB=1∶2,M为AB的中点,连结MD、MC,则∠DMC等于()A.30°B.60°C.90°D.45°4、如图,在□ABCD中,E为AD中点,CE交BA的延长线于F.(1)试证明:AB=AF.(2)若BC=2AB,∠FBC=70°,求∠EBC的度数5、如图,E、F是□ABCD对角线BD上的两点,请你添加一个适当的条件:________________,使得四边形AECF是平行四边形.并说明理由。等第日期4FDECBAFEDCBA