《幂函数》课件VIP免费

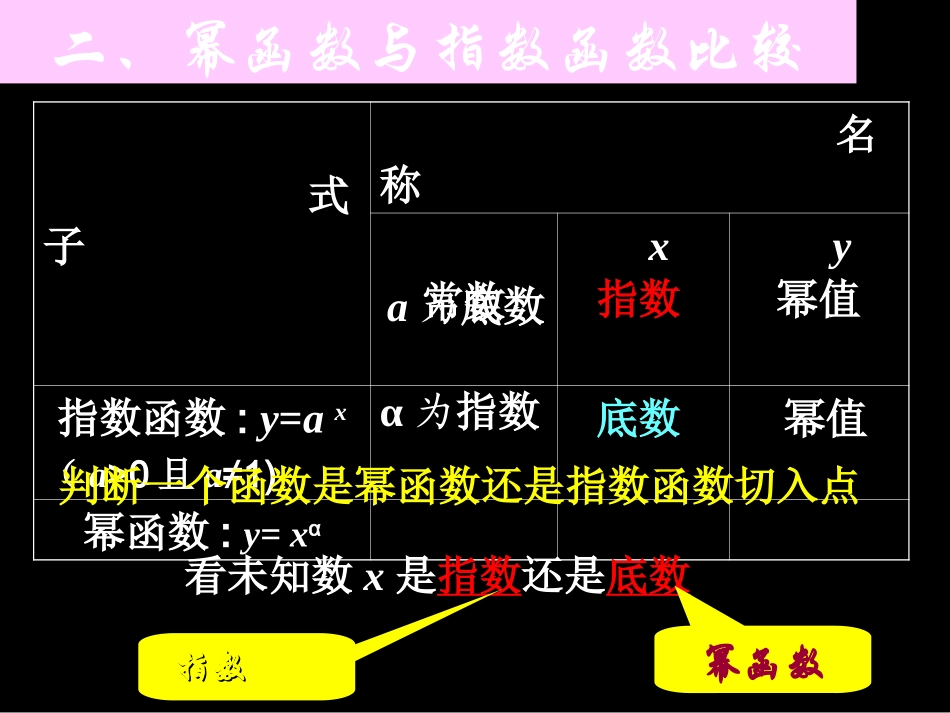
§2.3幂函数高中数学必修①人教版A一、幂函数的定义：一般地，我们把形如的函数叫做幂函数，其中为自变量，为常数。xyx练习1：判断下列函数哪几个是幂函数？xyxyxyxyyx1)5(;1)4(;2)3(;)2(;31222）（答案（2）（5）思考：指数函数y=ax与幂函数y=xα有什么区别？中前面的系数是中前面的系数是11，后面没，后面没有其它项。有其它项。xyx式子名称常数xy指数函数:y=ax（a>0且a≠1)幂函数:y=xαa为底数指数α为指数底数幂值幂值二、幂函数与指数函数比较判断一个函数是幂函数还是指数函数切入点看未知数x是指数还是底数幂函数指数指数函数。m，xmmxfm的值求是幂函数已知例3221)(:1例2：已知函数是幂函数,并且是偶函数，求m的值。22233)(mxmmxf。m，xmmxfm的值求是幂函数已知例3221)(:1是幂函数因为解)(:xf112mm12:mm或解之得12mm或xy2.0xy521xy1xy（指数函数）（幂函数）（指数函数）（幂函数）快速反应xy3（指数函数）5xy（幂函数）已知函数是幂函数,并且是偶函数，求m的值。22233)(mxmmxf练习1：1332mm12:mm或解之得是偶函数又因为)(xf舍去不符合题意，m12m1332mm12:mm或解之得1332mm是偶函数又因为)(xf12:mm或解之得1332mm舍去不符合题意，m1是偶函数又因为)(xf12:mm或解之得1332mm练习3：已知幂函数f(x)的图像经过点（3，27），求证：f(x)是奇函数。xy设所求的幂函数为证明:)273(，函数的图像过点,327333即333)()(xxxf3)(xxf)()(xfxfR，xf的定义域为)(是奇函数)(xf二、五个常用幂函数的图像和性质(1)(2)(3)(4)(5)21xy2xy1xy3xyxy定义域：值域：奇偶性：单调性：RR上是奇函数在R上是增函数在Rxy函数的图像定义域：值域：奇偶性：单调性：R),0[上是偶函数在R上是增函数在),0[上是减函数在]0,(函数的图像2xy定义域：值域：奇偶性：单调性：}0{xx上是奇函数在}0{xx上是减函数在),0(上是减函数在)0,(}0{yy函数的图像1xy?213的图像呢和如何画xyxy定义域：值域：奇偶性：单调性：),0[非奇非偶函数上是增函数在),0[),0[函数的图像21xyx…-2-101234…y=x3……y=x1/2……-8-10182723010xy1234-1-2-32468-2-4-6-8y=x3//64y=y=21x22定义域：值域：奇偶性：单调性：RR上是奇函数在R上是增函数在R函数的图像3xy21xy幂函数的定义域、值域、奇偶性和单调性，随常数α取值的不同而不同.y=x3定义域值域单调性公共点y=xRRR[0，+∞）R[0，+∞）R[0，+∞）奇函数偶函数奇函数非奇非偶函数奇函数在R上是增函数在（－∞,0]上是减函数，在(0,+∞）上是增函数在R上是增函数在(0，+∞)上是增函数在(－∞,0)，(0,+∞）上是减函数（1，1）奇偶性y=x21xy0，（0，+）0，（0，+）下面将5个函数的图像画在同一坐标系中(1)(2)(3)(4)(5)21xy2xy1xy3xyxy4321-1-2-3-4-22462yx3yx(1,1)(2,4)(-2,4)(-1,1)(-1,-1)yy==xx12yx1xy4321-1-2-3-4-6-4-2246y=x-1y=x12y=x3y=x2y=x(4,2)(-2,4)(2,4)(-1,1)(-1,-1)(1,1)在第一象限内，a>0,在(0,+∞)上为增函数;a<0,在(0,+∞)上为减函数.幂函数的图象都通过点(1,1)α为奇数时,幂函数为奇函数,α为偶数时,幂函数为偶函数.下列结论中正确的是A幂函数图像都经过点（0,0），（1,1）B幂函数图像不可能出现在第四象限C当n＞0的时候，幂函数y=xn的值随x的增大而增大。D当n=0的时候，幂函数y=xn的图像是一条直线。练习：利用单调性判断下列各值的大小。（1）5.20.8与5.30.8（2）0.20.3与0.30.3(3)2.5-25Óë2.7-25解:(1)y=x0.8在(0,∞)内是增函数, 5.2<5.3∴5.20.8<5.30.8(2)y=x0.3在(0,∞)内是增函数 0.2<0.30.2∴0.3<0.30.3(3)y=x-2/5在(0,∞)内是减函数 2.5<2.72.5∴-2/5>2.7-2/5比较各组数的大小3241413121218.0,6.2,5.2)2(1.1,4.1,1.1)1(练习3:如图所示，曲线是幂函数y=xk在第一象限内的图象，已知k分别取...