直线倾斜角与斜率VIP免费

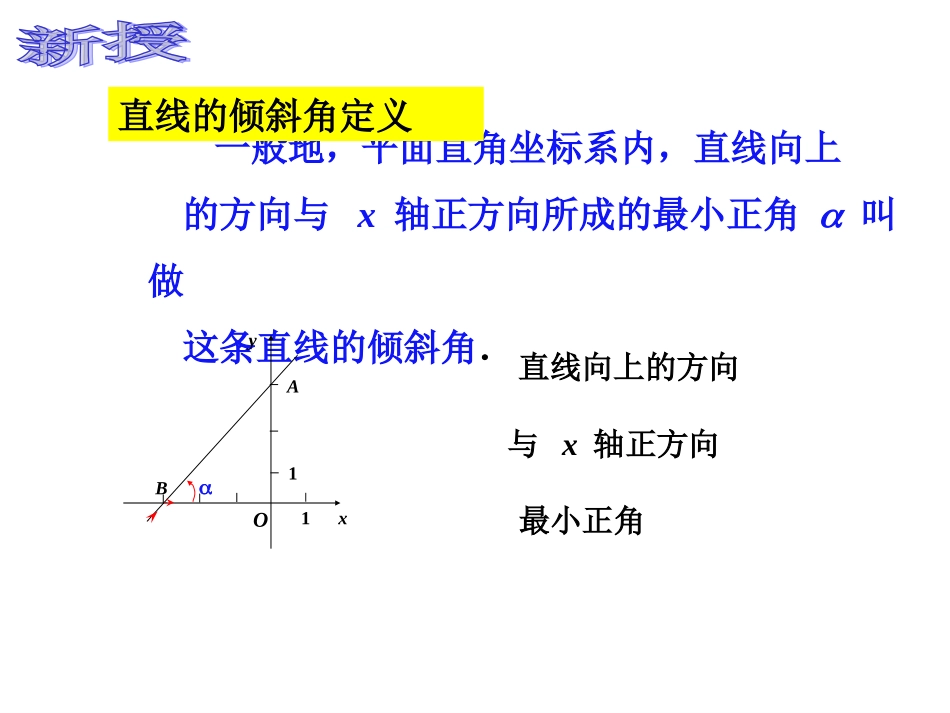
圆直线直线圆3.1.1直线的倾斜角与斜率我们知道，两点确定一条直线．一点能确定一条直线的位置吗？已知直线l经过点P，直线l的位置能够确定吗？问题引入问题引入xyOll’l’’P一般地，平面直角坐标系内，直线向上的方向与x轴正方向所成的最小正角叫做这条直线的倾斜角．xyBAO11直线的倾斜角定义直线向上的方向与x轴正方向最小正角一般地，平面直角坐标系内，直线向上的方向与x轴正向所成的最小正角叫做这条直线的倾斜角．规定：当直线和x轴平行或重合时，它的倾斜角为0°直线的倾斜角定义倾斜角的范围：0≤<180xyBAO11X.pYOX.pYOX.pYOX.pYO（1）（2）（4）（3）900oo009000018090练习：xyoxyoxyoxyo（A）（B）（C）（D）下列图中标出的直线的倾斜角对不对？如果不对，违背了定义中的哪一条？日常生活中，还有没有表示倾斜程度的量？前进量升高量水平长度铅直高度坡度结论：坡度越大，楼梯越陡．0.8m1m0.4m倾斜角不是90的直线，它的倾斜角的正切值叫做这条直线的斜率，通常用k表示，即直线的斜率定义k＝tan．练习一已知直线的倾斜角，求对应的斜率k：（1）＝0；（2）＝30；（3）＝135；（4）＝120．X.pYOX.pYOX.pYOX.pYO（1）（2）（4）（3）900ooK>0K<0K不存在K=0001809000900的定义＝tanα求出直线的斜率；k如果给定直线的倾斜角，我们当然可以根据斜率如果给定直线上两点坐标，直线是确定的，倾斜角也是确定的，斜率就是确定的，那么又怎么求出直线的斜率呢？已知两点P1(x1，y1)、P2(x2，y2)（其中x1≠x2），求直线P1P2的斜率?探究：),(111yxP),(222yxP,12QPP如图，α为锐角xyo1x2x1y2y),(12yxQ中在QPPRt12QPQPQPPk1212tantan1212xxyyxyo),(111yxP),(222yxP),(12yxQ如图α为钝角，,180tan)180tan(tan中在12QPPRtQPQP12tan2112xxyy12122112tanxxyyxxyyk1x2x1y2yxyo),(111yxP),(222yxP1y2y1212xxyyk答：斜率不存在，因为分母为0。当直线与坐标轴平行或重合时,上述公式还适用吗？oyxl222(,)Pxy111(,)Pxy21210yykxx3.斜率公式公式的特点:(1)与两点的顺序无关;(2)公式表明,直线的斜率可以通过直线上任意两(3)当x1=x2时,公式不适用,此时α=900点的坐标来表示,而不需要求出直线的倾斜角211221()yykxxxx111222(,),(,)PxyPxy经过两点的直线的斜率公式例1：已知点，01AB（3，2），（-4，1），C（，）(1).求直线AB，BC，CA的斜率，并判断这些直线的倾斜角是锐角还是钝角OxyACB12114371110(4)212103ABBCCAkkk解：（）12]2（）k[1,+)(-,-(2).过点C的直线与线段ＡＢ有公共点，求的斜率k的取值范围ll锐角钝角锐角例2、在平面直角坐标系中，画出经过原点且斜率分别为1，-1，2和-3的直线。例题分析例题分析4321,,llll及Oxy3l1l2l4lA3A1A2A4(1,1)(1,-1)(1,2)(1,-3)下列哪些说法是正确的A、任一条直线都有倾斜角，不是锐角就是直角或钝角。B、直线的倾斜角越大，斜率也越大C、两直线的倾斜角相等，它们的斜率也相等，反之也成立。D、任何直线都有倾斜角，但不一定都有斜率E、直线集合与集合{a|0°≤a<180°}建立了一一对应的关系(D)（1）直线的倾斜角的范围为_______直线斜率的范围为____（5）直线L过点（m,n）和原点，（m≠0)则L的斜率为____。（3）若直线的斜率是-1，则直线的倾斜角为____。（2）若直线L向上的方向与y轴正方向的夹角为30°，则直线倾斜角为____斜率为____。达标演练（4）已知直线的斜率为k,倾斜角为a，-1≤k≤1则的范围为_______；若k≥1或k≤-1,则a的范围为________。60°135°34,043,2,432,4mn,0R•已知A(-3,-5),B(1,3),C(5,11)三点，证明这三点在同一条直线上。解析：23153xxyykABABAB215311xxyykBCBCBCkkBCAB直线AB与BC平行，又因为直线AB与BC过同一点B,所以直线AB与BC重合，A.B.C三点在一...