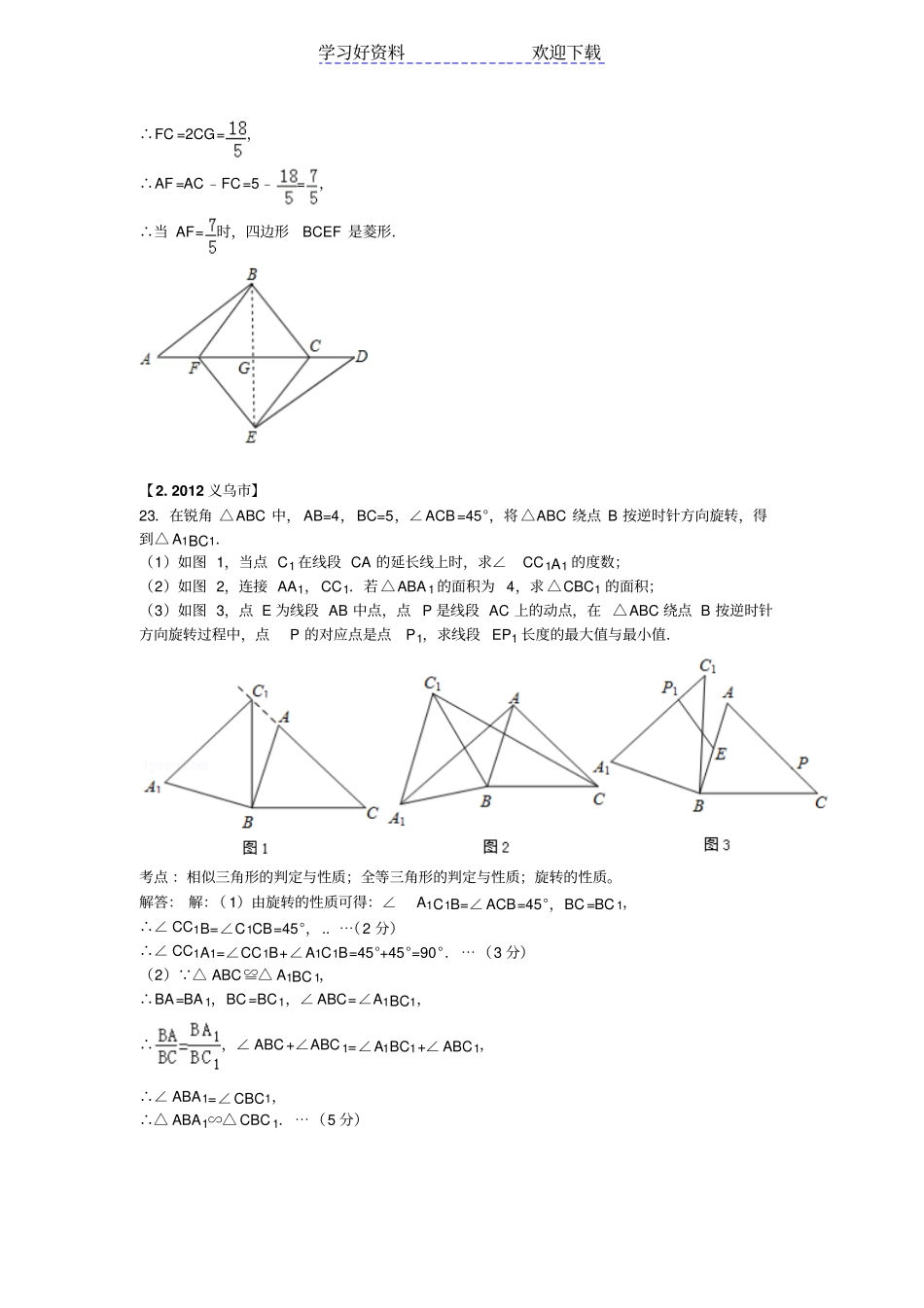
学习好资料欢迎下载20XX年各地中考数学汇编三角形四边形精选(1~10)【1.2012临沂】22.如图,点A.F、C.D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.(1)求证:四边形BCEF是平行四边形,(2)若∠ABC=90°,AB=4,BC=3,当AF为何值时,四边形BCEF是菱形.考点:相似三角形的判定与性质;全等三角形的判定与性质;勾股定理;平行四边形的判定;菱形的判定。解答:(1)证明: AF=DC,∴AF+FC=DC+FC,即AC=DF.在△ABC和△DEF中,,∴△ABC≌DEF(SAS),∴BC=EF,∠ACB=∠DFE,∴BC∥EF,∴四边形BCEF是平行四边形.(2)解:连接BE,交CF与点G, 四边形BCEF是平行四边形,∴当BE⊥CF时,四边形BCEF是菱形, ∠ABC=90°,AB=4,BC=3,∴AC==5, ∠BGC=∠ABC=90°,∠ACB=∠BCG,∴△ABC∽△BGC,∴=,即=,∴CG=, FG=CG,学习好资料欢迎下载∴FC=2CG=,∴AF=AC﹣FC=5﹣=,∴当AF=时,四边形BCEF是菱形.【2.2012义乌市】23.在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;(2)如图2,连接AA1,CC1.若△ABA1的面积为4,求△CBC1的面积;(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1,求线段EP1长度的最大值与最小值.考点:相似三角形的判定与性质;全等三角形的判定与性质;旋转的性质。解答:解:(1)由旋转的性质可得:∠A1C1B=∠ACB=45°,BC=BC1,∴∠CC1B=∠C1CB=45°,..⋯(2分)∴∠CC1A1=∠CC1B+∠A1C1B=45°+45°=90°.⋯(3分)(2) △ABC≌△A1BC1,∴BA=BA1,BC=BC1,∠ABC=∠A1BC1,∴,∠ABC+∠ABC1=∠A1BC1+∠ABC1,∴∠ABA1=∠CBC1,∴△ABA1∽△CBC1.⋯(5分)学习好资料欢迎下载∴, S△ABA1=4,∴S△CBC1=;⋯(7分)(3)过点B作BD⊥AC,D为垂足, △ABC为锐角三角形,∴点D在线段AC上,在Rt△BCD中,BD=BC×sin45°=,⋯(8分)①如图1,当P在AC上运动至垂足点D,△ABC绕点B旋转,使点P的对应点P1在线段AB上时,EP1最小,最小值为:EP1=BP1﹣BE=BD﹣BE=﹣2;⋯(9分)②当P在AC上运动至点C,△ABC绕点B旋转,使点P的对应点P1在线段AB的延长线上时,EP1最大,最大值为:EP1=BC+AE=2+5=7.⋯(10分)【3.2012?杭州】21.如图,在梯形ABCD中,AD∥BC,AB=CD,分别以AB,CD为边向外侧作等边三角形ABE和等边三角形DCF,连接AF,DE.(1)求证:AF=DE;(2)若∠BAD=45°,AB=a,△ABE和△DCF的面积之和等于梯形ABCD的面积,求BC的长.学习好资料欢迎下载考点:等腰梯形的性质;全等三角形的判定与性质;等边三角形的性质。专题:探究型。分析:(1)根据等腰梯形的性质和等边三角形的性质以及全等三角形的判定方法证明△AED≌△DFA即可;(2)如图作BH⊥AD,CK⊥AD,利用给出的条件和梯形的面积公式即可求出BC的长.解答:(1)证明:在梯形ABCD中,AD∥BC,AB=CD,∴∠BAD=∠CDA,而在等边三角形ABE和等边三角形DCF中,AB=AE,DC=DF,且∠BAE=∠CDF=60°,∴AE=DF,∠EAD=∠FDA,AD=DA,∴△AED≌△DFA(SAS),∴AF=DE;(2)解:如图作BH⊥AD,CK⊥AD,则有BC=HK, ∠BAD=45°,∴∠HAB=∠KDC=45°,∴AB=BH=AH,同理:CD=CK=KD, S梯形ABCD=,AB=a,∴S梯形ABCD==,而S△ABE=S△DCF=a2,∴=2×a2,∴BC=a.学习好资料欢迎下载点评:本题综合性的考查了等腰梯形的性质、等边三角形的性质、全等三角形的判定、全等三角形的性质以及等于直角三角形的性质和梯形、三角形的面积公式,属于中档题目.【4.2012?烟台】25.(1)问题探究如图1,分别以△ABC的边AC与边BC为边,向△ABC外作正方形ACD1E1和正方形BCD2E2,过点C作直线KH交直线AB于点H,使∠AHK=∠ACD1作D1M⊥KH,D2N⊥KH,垂足分别为点M,N.试探究线段D1M与线段D2N的数量关系,并加以证明.(2)拓展延伸①如图2,若将“问题探究”中的正方形改为正三角形,过点C作直线K1H1,K2H2,分别交直线AB于点H1,H2,使∠AH1K1=∠BH2K2=∠ACD1.作D1M⊥K1H1,D2N⊥K2H2,垂足分别为点M,N.D1M=D2N是...