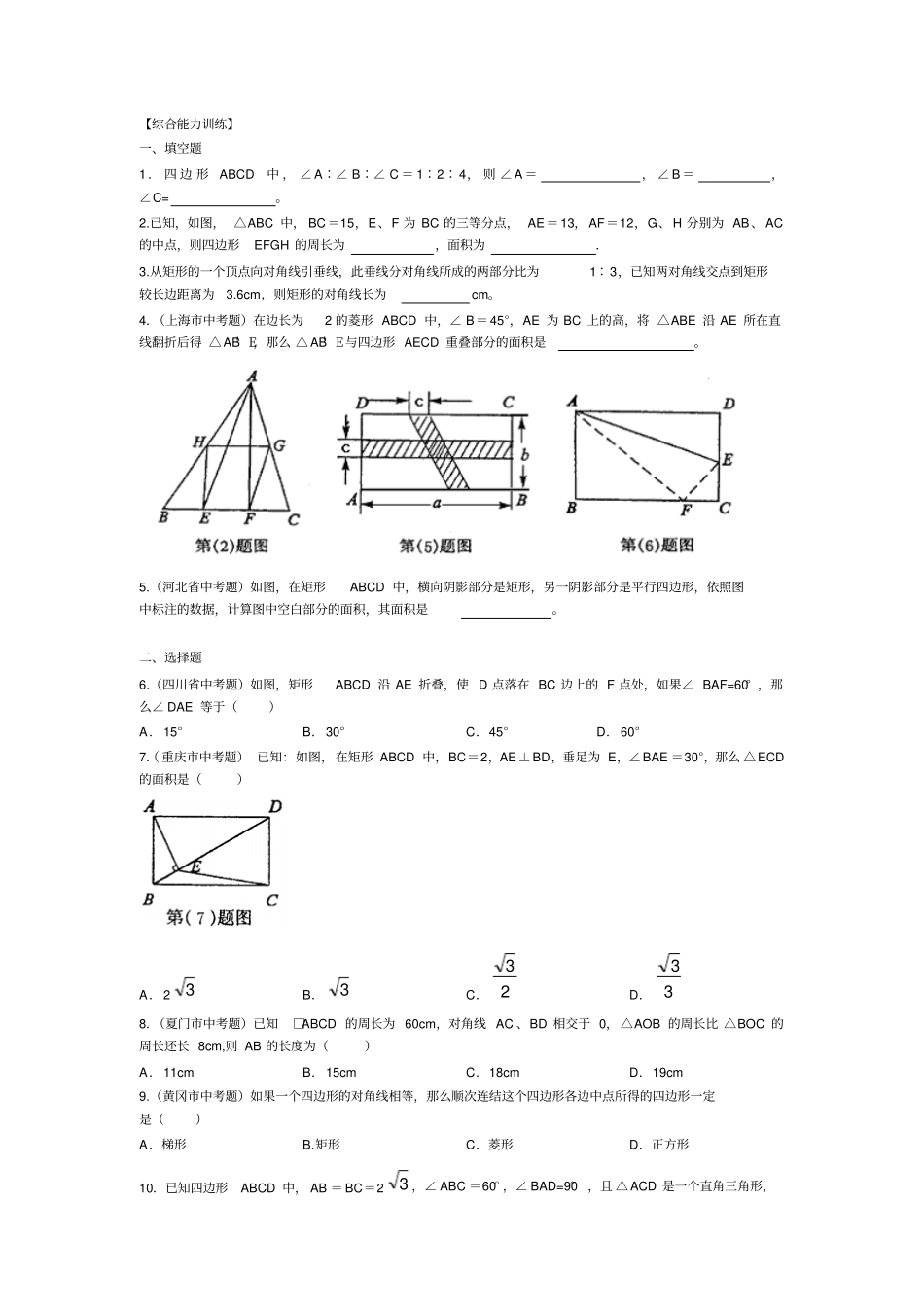
中考四边形专题复习难点:综合运用平行四边形、特殊的平行四边形和三角形的有关知识进行四边形或多边形的有关证明或计算.考点:平行四边形和特殊的平行四边形的有关知识,在近几年各地中考试题中考查较多,约占考量的7%左右,必须予以足够的重视.【经典范例引路】例1已知,如图,在平行四边形ABCD中,E是CD的中点,F是AE的中点,FC与BE相交于G,求证:GF=GC.证明:如图,过点F作FH∥AB交BE于点H,连结CH, EF=FA,∴EH=HB,∴FH∥21AB,又点E是DC的中点,∴EC=21DC,又AB∥DC,∴FH∥EC.∴四边形EFHC是平行四边形,∴GF=GC.【解题技巧点拨】本题综合运用了三角形的中位线的判定和性质,平行四边形的判定和性质使问题得到解决,而其中通过作平行线FH∥AB构造平行四边形EFHC是使问题获得证明的关键.例2已知:如图在△ABC中,∠C=90°,CF是斜边上的高,AT平分∠CAB,交CF于点D,过D作DE∥AB交BC于E,求证:CT=BE.证明:如图,过点T作TG⊥AB于G,连结DG. CF⊥AB,∴TG∥CF,又AT平分∠CAB,TC⊥CA,TG⊥AB。∴CT=TG, ∠CDT=∠1+∠2,∠CTD=∠3+∠B,又∠2=∠3,∠1=∠B,∴∠CDT=∠CTD,∴CT=CD,∴CD=CT=TG,又CD∥TG,∴四边形CDGT是菱形.∴CT=DG,且CB∥DG,又DE∥AB,∴四边形DEBG是平行四边形,∴DG=BE,故CT=BE.【解题技巧点拨】本题在证明过程中,综合运用了角平分线的性质,菱形的判定和性质,平行四边形的判定和性质等知识,有一定的技巧性和难度,而其中的关键是通过作辅助线构造菱形CDGT和□DEBG。【综合能力训练】一、填空题1.四边形ABCD中,∠A∶∠B∶∠C=1∶2∶4,则∠A=,∠B=,∠C=。2.已知,如图,△ABC中,BC=15,E、F为BC的三等分点,AE=13,AF=12,G、H分别为AB、AC的中点,则四边形EFGH的周长为,面积为.3.从矩形的一个顶点向对角线引垂线,此垂线分对角线所成的两部分比为1∶3,已知两对角线交点到矩形较长边距离为3.6cm,则矩形的对角线长为cm。4.(上海市中考题)在边长为2的菱形ABCD中,∠B=45°,AE为BC上的高,将△ABE沿AE所在直线翻折后得△AB′E,那么△AB′E与四边形AECD重叠部分的面积是。5.(河北省中考题)如图,在矩形ABCD中,横向阴影部分是矩形,另一阴影部分是平行四边形,依照图中标注的数据,计算图中空白部分的面积,其面积是。二、选择题6.(四川省中考题)如图,矩形ABCD沿AE折叠,使D点落在BC边上的F点处,如果∠BAF=60°,那么∠DAE等于()A.15°B.30°C.45°D.60°7.(重庆市中考题)已知:如图,在矩形ABCD中,BC=2,AE⊥BD,垂足为E,∠BAE=30°,那么△ECD的面积是()A.23B.3C.23D.338.(夏门市中考题)已知□ABCD的周长为60cm,对角线AC、BD相交于0,△AOB的周长比△BOC的周长还长8cm,则AB的长度为()A.11cmB.15cmC.18cmD.19cm9.(黄冈市中考题)如果一个四边形的对角线相等,那么顺次连结这个四边形各边中点所得的四边形一定是()A.梯形B.矩形C.菱形D.正方形10.已知四边形ABCD中,AB=BC=23,∠ABC=60°,∠BAD=90°,且△ACD是一个直角三角形,那么AD的长等于()A.3B.4C.3或4D.611.菱形的周长为2a,两条对角线之和为b,则菱形面积为()A.b2-a2B.222abC.422abD.822ab12.一个平行四边形的两条对角线的长度分别为5和7,则它的一条边长a的取值范围是()A.1<a<6B.1≤a≤6C.2<a<6D.2<a<12三、解答下列各题13.已知,如图,正方形ABCD的边长为16,F在AD上,CE⊥CF交AB的延长线于E,且△CEF的面积为200,求BE的长.14.(苏州市中考题)如图,已知E为□ABCD中DC边的延长线上的一点,且CE=CD,连接AE分别交BC、BD于点F、G.(1)求证:△AFB≌△EFC;(2)若BD=12cm,求DG的长.15.如图,矩形ABCD中,AB=8cm,AD=6cm,点O是矩形对角线的交点,过点O任作一直线l,分别过点A、C作l的垂线,垂足为E、F,(1)求证:AE=CF;(2)当直线l满足什么条件时,垂线段CF的长达到最大值?最大值为多少?16.已知如图,AD是△ABC的中线,点G在AD上,AG=2GD,连结BG,CG并延长,分别交AC,AB于E、F,(1)求证:E、F分别是AC、AB边的中点,(2)MN是△GBC的中...