弹性力学 极坐标求解VIP免费

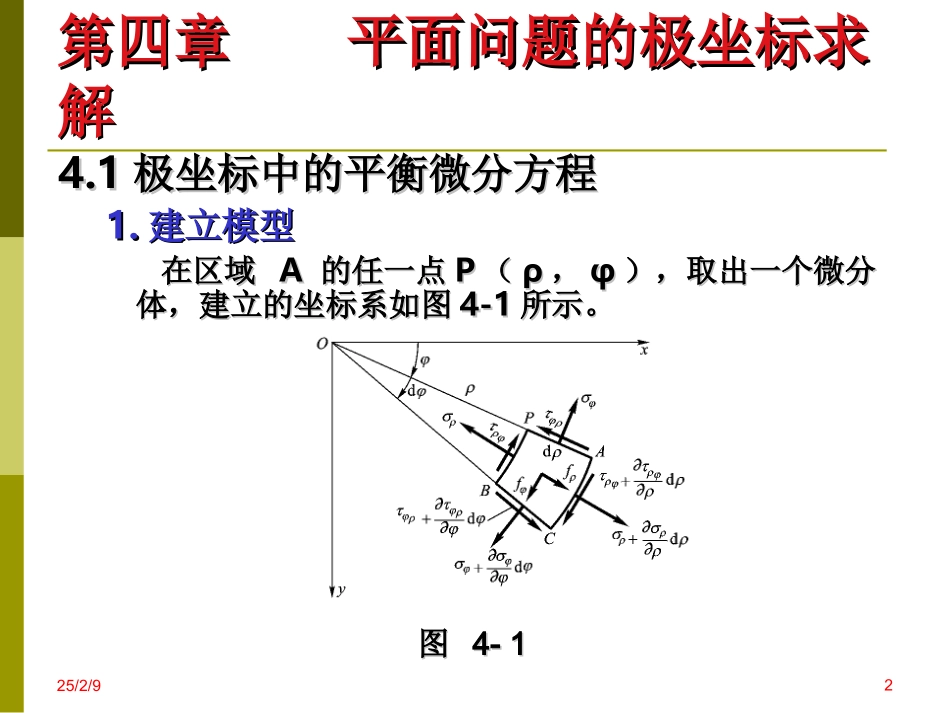
本章重点本章重点（1）掌握在极坐标系中基本方程的建立；（2）掌握极坐标系中平面问题按应力求解的方法；（3）了解极坐标系中与直角坐标系中的基本方程的相似之处和不同之处；（4）掌握用极坐标对圆环或圆筒均布压力、压力隧洞、圆孔孔口应力集中、半平面体在边界上受集中力或受分布力时的解答。第四章平面问题的极坐标求第四章平面问题的极坐标求解解25/2/9125/2/924.14.1极坐标中的平衡微分方程极坐标中的平衡微分方程1.1.建立模型建立模型在区域在区域AA的任一点的任一点PP（（ρρ，，φφ），取出一个微分），取出一个微分体，建立的坐标系如图体，建立的坐标系如图4-14-1所示。所示。图图4-14-1第四章平面问题的极坐标求第四章平面问题的极坐标求解解2.正负符号的规定（（11））在极坐标中，在极坐标中，ρρ从原点出发，以向外为正；从原点出发，以向外为正；而而φφ以以xx轴正向到轴正向到yy轴正向的转向为正；轴正向的转向为正；（（22））应力的表示和符号规定与直角坐标相同，应力的表示和符号规定与直角坐标相同，仍以正面正向，负面负向的应力为正，反之为负；仍以正面正向，负面负向的应力为正，反之为负；（（33））微分体上的体力为和，表示于微分微分体上的体力为和，表示于微分体的中心，分别沿径向和环向，以沿正坐标方向体的中心，分别沿径向和环向，以沿正坐标方向为正，反之为负。为正，反之为负。25/2/93第四章平面问题的极坐标求第四章平面问题的极坐标求解解ρfφf第四章平面问题的极坐标求第四章平面问题的极坐标求解解3.3.列平衡方程求解列平衡方程求解由可得由可得由可得由可得sinsin22coscos022ddddddddddddddfdd0F0Fcoscos22sinsin022ddddddddddddddfdd25/2/94化简以上两式，由于微小，可以把化简以上两式，由于微小，可以把另外在上式中，另外在上式中，分别出现了一、二、三阶微量，其中一阶微量互分别出现了一、二、三阶微量，其中一阶微量互相抵消，二阶微量保留，而将更高阶的三阶微量相抵消，二阶微量保留，而将更高阶的三阶微量略去。化简可得：略去。化简可得：25/2/95sindφ2取为,把取为1dφdφcos22用代替，10210ff（（4-14-1））第四章平面问题的极坐标求第四章平面问题的极坐标求解解d4.4.直角坐标与极坐标比较直角坐标与极坐标比较1.1.在（在（4-14-1）的第一式中，前两项与直角坐标的相似；）的第一式中，前两项与直角坐标的相似；而项是由于正而项是由于正ρρ面的面积大于负面的面积大于负ρρ面而产生的，面而产生的，是由于正负是由于正负φφ面上的正应力在通过微分体中心的面上的正应力在通过微分体中心的ρρ方向方向有投影而引起的。有投影而引起的。2.2.在式（在式（4-14-1）的第二式中，前两项也与直角坐标的相）的第二式中，前两项也与直角坐标的相似；而是由于正似；而是由于正ρρ面面积大于负面面积大于负ρρ面而产生的；面而产生的；是由于正负是由于正负φφ面上的切应力在通过微分体中心的面上的切应力在通过微分体中心的φφ方方向有投影而引起的。由于我们仍将这向有投影而引起的。由于我们仍将这两个切应力只作为一个未知函数处理。两个切应力只作为一个未知函数处理。625/2/9ρσρσ-ρρρτ=τ第四章平面问题的极坐标求第四章平面问题的极坐标求解解4.24.2极坐标中的几何方程及物理方程极坐标中的几何方程及物理方程1.1.几何方程的推导几何方程的推导（（11））建立坐标系建立坐标系在区域内任取一点在区域内任取一点PP（（ρρ，，φφ））作两个沿正标向的微分线作两个沿正标向的微分线段...