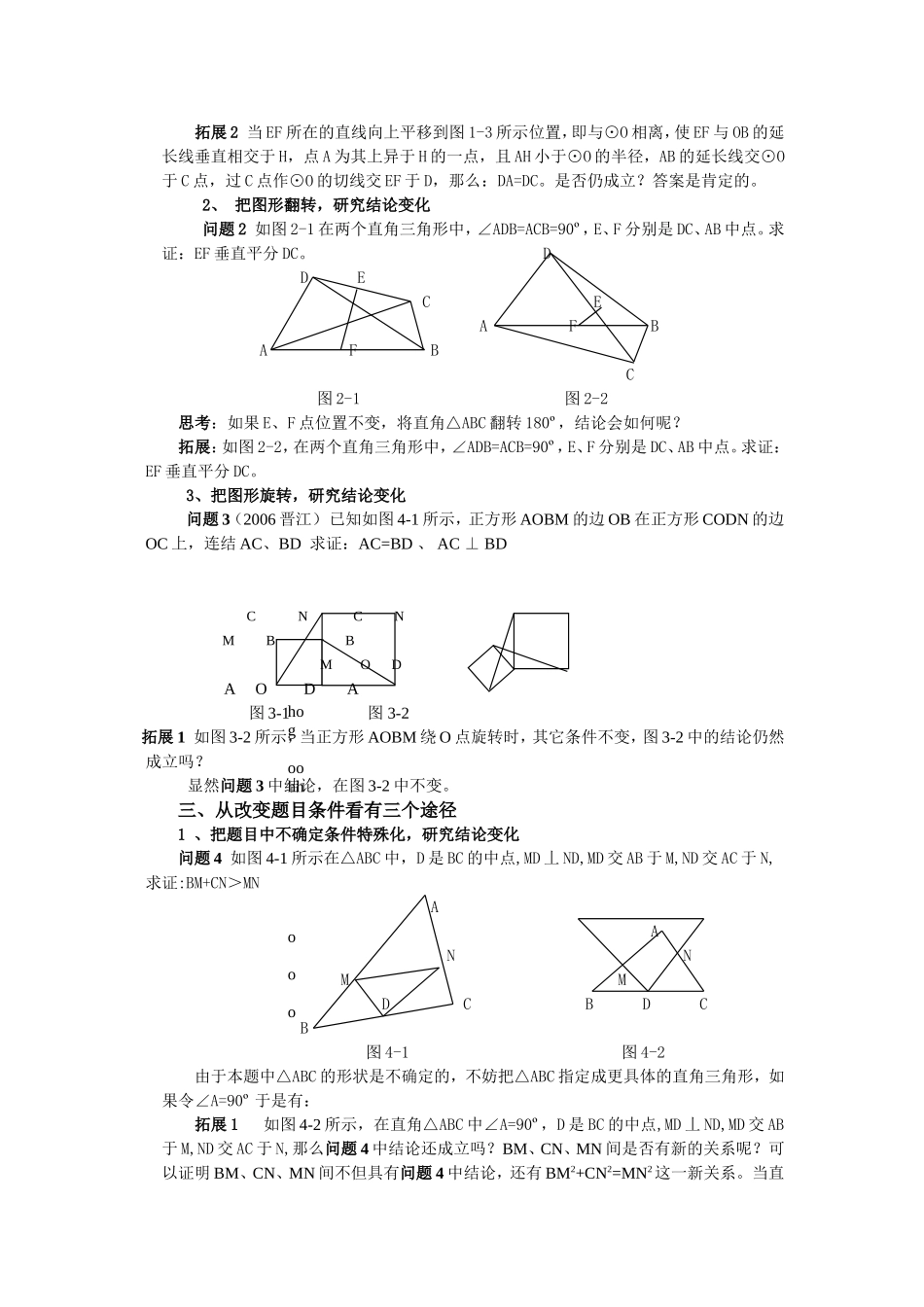
——浅谈几何习题挖掘的途径安徽省安庆市宜秀区五横初级中学戴向阳邮编246051手机13225725503有些几何题具有一定弹性、典型性、探索性,有拓展、开发和挖掘的余地与空间。把这类题进行适当地变换、延伸、拓展,一方面起到举一反三、完善知识结构、梳理知识网络的作用,另一方面培养了学生创新能力和敢于猜想、勇于探索的创新精神,增强了学生学习兴致,激发了学生求知欲,提高了学生探究能力。开拓学生视野、丰富学生思维,实现“不同人学不同数学”,体现“不同人在数学上得到不同发展”,凸现从“被动”接受式学习向“主动”探究性学习转变。下面笔者就自已教学实际谈谈如何具体重整、组合、拓展几何习题,以飨读者,愿与读者共勉之。挖潜几何习题,可从以几方面考虑:一、从认识事物方法上看有两个途径笔者在教学实践中发现,几何的曰常教学、尤其复习教学,要遵循这样原则:从一般到特殊或从特殊到一般地“挖潜”问题。如此一来既在面上拓广了知识点间的横向联系,又在深度上延伸了知识的纵向认识。因此,教师“挖潜”问题可考虑从此两个方向入手。前者犹如出发旅游,一路风景逐渐引人入胜,会有“晋人”发现桃花源惊喜不断,越探究越能激发学生学习激情和求知欲,越能发现问题丰富多彩的外在形式,拓深问题的外延,从而纵深把握问题,踩中中考命题的思路。毋庸讳言,中考中一些较好几何题,总是从以往的某些中考题中或课本中习题、练习、例题中拓展得来的。换言之,中考中比较有特色几何题,具有纵深发展性。另外拓展知识外延也是人们获取新知的一个重要来源,从这点看,教学中贯彻从一般到特殊的探究问题方法,实则“授人以渔”。从特殊到一般,就要求教师要有较深的数学专业素养,能从大量相似问题中发现共同点,本质联系,从而删繁就简,浓缩问题,提炼问题,形成一般性结论。从而传给学生的不是一个孤立题目或几个题目,而是一类问题的解法。从一般到特殊,从特殊到一般,有利于培养学生举一反三、触类旁通的自建构智能。从一般到特殊、从特殊到一般是辨证的,是数学统一美、和谐美的要求和体现。它有利于增进学生对数学的兴趣,激发求知欲,从而主动贴近数学,愉快地获取数学知识。如何从一般到特殊或从特殊到一般拓展成题,笔者在此不再引例具体赘述,下面,笔者借助例子,谈谈在具体方面的拓展途径,读者也可从中,就如何从一般到特殊或从特殊到一般窥豹一斑。二、从图形变换方面看有三个途径1、把图形平移,研究结论变化问题1(几何课本第三册第199页11题)如图1-1,A为⊙O的直径EF上的一点,OB是和这条直径垂直的半径,BA和⊙O相交于另一点C,过点C的切线和EF的延长线相交于点D,求证:DA=DC。BBEDHAFBEOAFDEHAFDOCOCC图1-1图1-2图1-3拓展1将图1-1中直径EF所在的直线向上平移到图1-2所示位置,这时OB与EF垂直相交于H,其它条件不变。可证:DA=DC。hogoohhooo拓展2当EF所在的直线向上平移到图1-3所示位置,即与⊙O相离,使EF与OB的延长线垂直相交于H,点A为其上异于H的一点,且AH小于⊙O的半径,AB的延长线交⊙O于C点,过C点作⊙O的切线交EF于D,那么:DA=DC。是否仍成立?答案是肯定的。2、把图形翻转,研究结论变化问题2如图2-1在两个直角三角形中,∠ADB=ACB=90º,E、F分别是DC、AB中点。求证:EF垂直平分DC。DDECEAFBAFBC图2-1图2-2思考:如果E、F点位置不变,将直角△ABC翻转180º,结论会如何呢?拓展:如图2-2,在两个直角三角形中,∠ADB=ACB=90º,E、F分别是DC、AB中点。求证:EF垂直平分DC。3、把图形旋转,研究结论变化问题3(2006晋江)已知如图4-1所示,正方形AOBM的边OB在正方形CODN的边OC上,连结AC、BD求证:AC=BD、AC⊥BDCNCNMBBMODAODA图3-1图3-2拓展1如图3-2所示,当正方形AOBM绕O点旋转时,其它条件不变,图3-2中的结论仍然成立吗?显然问题3中结论,在图3-2中不变。三、从改变题目条件看有三个途径1、把题目中不确定条件特殊化,研究结论变化问题4如图4-1所示在△ABC中,D是BC的中点,MD丄ND,MD交AB于M,ND交AC于N,求证:BM+CN>MNAANNMMDCBDCB图4-1图4-2由于本题中△ABC的形状是不确定的,不妨把△ABC指定成更具体的直角三角形,如果令∠A=90º...