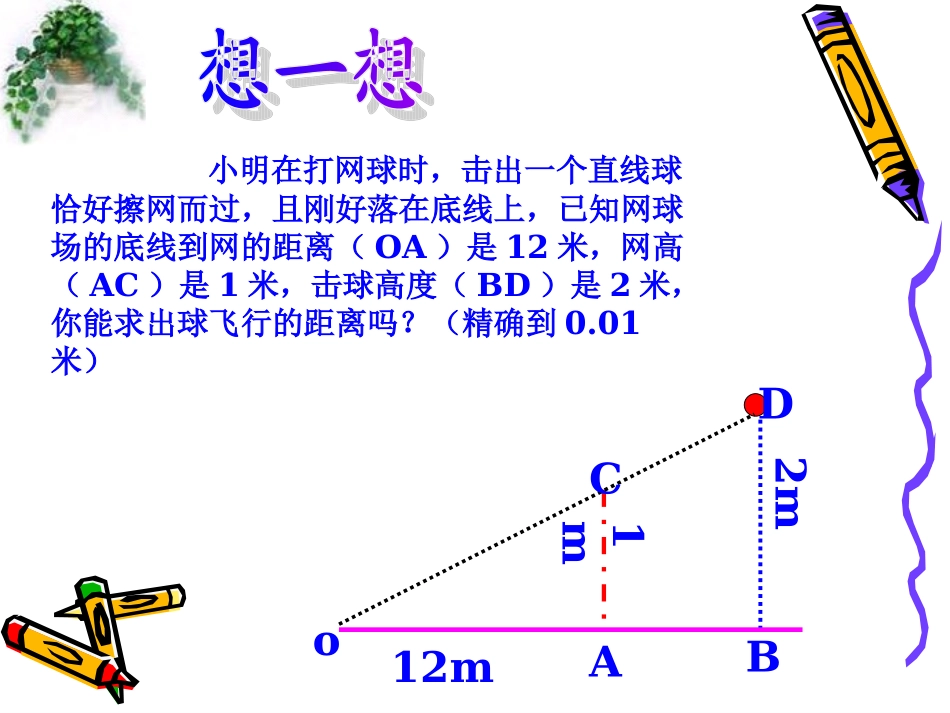
红旗农场中学高连世oABCD12m1m2m小明在打网球时,击出一个直线球恰好擦网而过,且刚好落在底线上,已知网球场的底线到网的距离(OA)是12米,网高(AC)是1米,击球高度(BD)是2米,你能求出球飞行的距离吗?(精确到0.01米)小明在打网球时,击出一个直线球恰好擦网而过,且刚好落在底线上,已知网球场的底线到网的距离(OA)是12米,网高(AC)是1米,击球高度(BD)是2米,你能求出球飞行的距离吗?(精确到0.01米)若小明第二次击的直线球仍擦网而过且刚好落在底线上,击球高度(B1D1)是3米这时球飞行的距离是多少米?球的飞行直线与地面的夹角有变化吗?击球高度与球飞行的距离比值有变化吗?oABCD12m1m2mB1D13m请各组分别度量这两幅三角板的斜边和每个锐角所对边的长,并计算每个锐角的对边与斜边的比值你能发现什么规律吗?(1)直角三角形中,锐角大小确定后,这个角的对边与斜边的比值随之确定;(2)直角三角形中一个锐角的度数越大,它的对边与斜边的比值越大ABCa对边(C斜边b直角三角形的一个锐角的对边与斜边的比值为这个锐角的正弦如:∠A的正弦sinA=∠A的对边斜边ac=即记作:sinA1、再Rt△ACB,Rt△DEF中,∠B=300,∠D=450,∠C=900,∠F=900,若AB=DE=2,(1)求∠B的对边与斜边的比值;(2)求∠A的对边与斜边的比值;(3)求∠D的对边与斜边的比值.ACBDEF我们利用三角板验证300、450、600角的正弦值及其变化的规律,那么对于00到900的其他锐角是否也满足这样的规律呢?(2)在Rt△ABC中,∠C=900,求sinA和sinB得值。BAC513ABC34(1)(2)已知Rt△ABC中,∠C=900。(1)若AC=4,AB=5,求sinA与sinB;(2)若AC=5,AB=12,求sinA与sinB;(3)若BC=m,AC=n,求sinB。本节课你有什么收获呢?1、习题28.1第一题2、补充作业在Rt△ABC中,∠C=900(1)AB=13,AC=12,求sinA(2)BC=8,AC=15,求sinAsinB(3)AB=10,BC=8,求sinAsinB