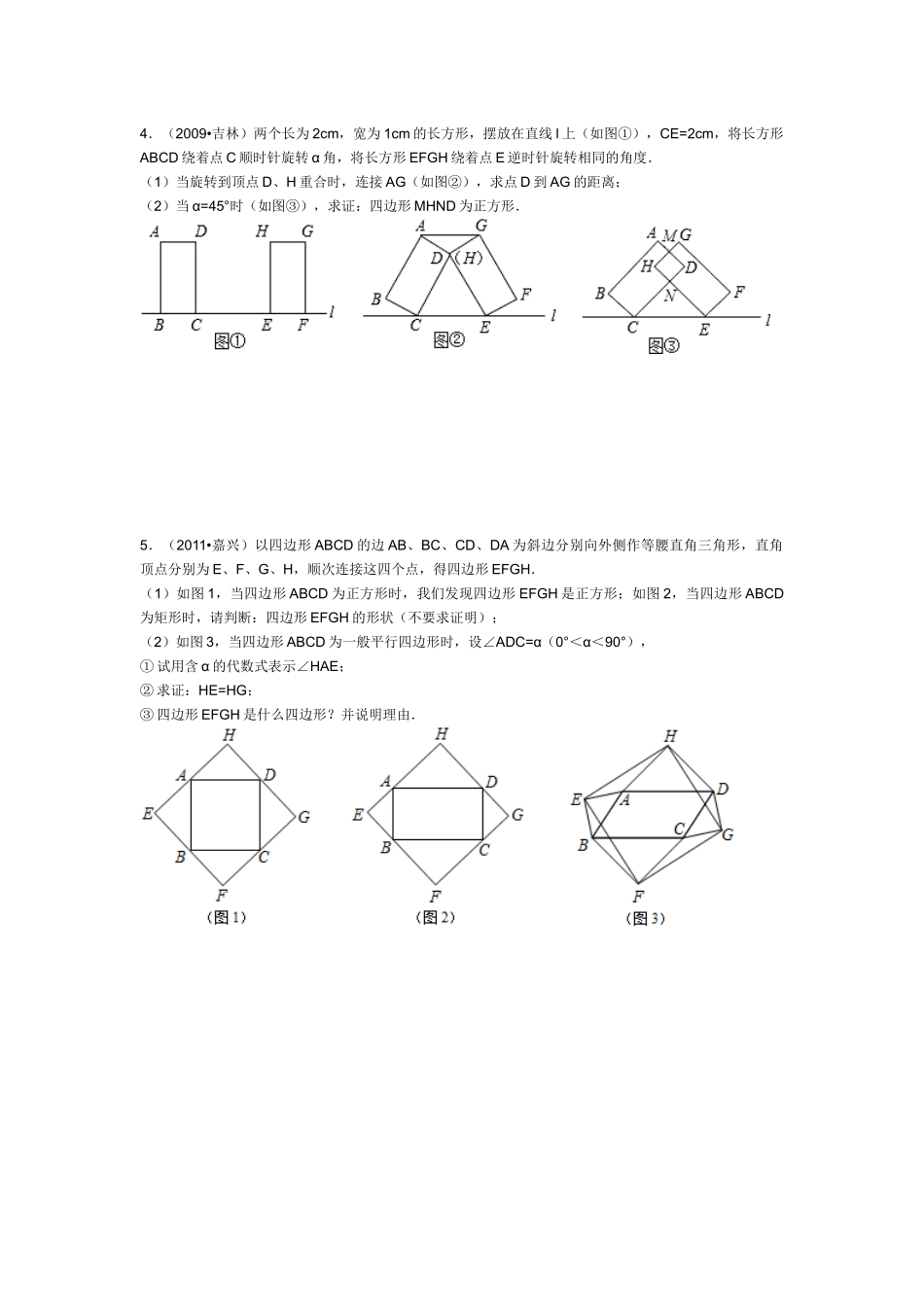
八年级兴趣小组数学试卷2013.3.261.如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为8,则BE=.2.如图,正方形ABCD的顶点A、B分别在x轴、y轴的正半轴上,反比例函数y=kx(k>0)的图象经过另外两个顶点C、D,且点D(4,n)(0<n<4),则k的值为()A.12B.8C.6D.43.一次函数y=ax+b的图象分别与x轴、y轴交于点M,N,与反比例函数y=kx的图象相交于点A,B.过点A分别作AC⊥x轴,AE⊥y轴,垂足分别为C,E;过点B分别作BF⊥x轴,BD⊥y轴,垂足分别为F,DAC与BD交于点K,连接CD.对于下述结论:①S四边形AEDK=S四边形CFBK;②AN=BM.③AB∥CD;不论点A,B在反比例函数y=kx的图象的同一分支上(如图1);还是点A,B分别在反比例函数y=kx的图象的不同分支上(如图2),都正确的是()A.①②B.①③C.②③D.①②③4.(2009•吉林)两个长为2cm,宽为1cm的长方形,摆放在直线l上(如图①),CE=2cm,将长方形ABCD绕着点C顺时针旋转α角,将长方形EFGH绕着点E逆时针旋转相同的角度.(1)当旋转到顶点D、H重合时,连接AG(如图②),求点D到AG的距离;(2)当α=45°时(如图③),求证:四边形MHND为正方形.5.(2011•嘉兴)以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,顺次连接这四个点,得四边形EFGH.(1)如图1,当四边形ABCD为正方形时,我们发现四边形EFGH是正方形;如图2,当四边形ABCD为矩形时,请判断:四边形EFGH的形状(不要求证明);(2)如图3,当四边形ABCD为一般平行四边形时,设∠ADC=α(0°<α<90°),①试用含α的代数式表示∠HAE;②求证:HE=HG;③四边形EFGH是什么四边形?并说明理由.