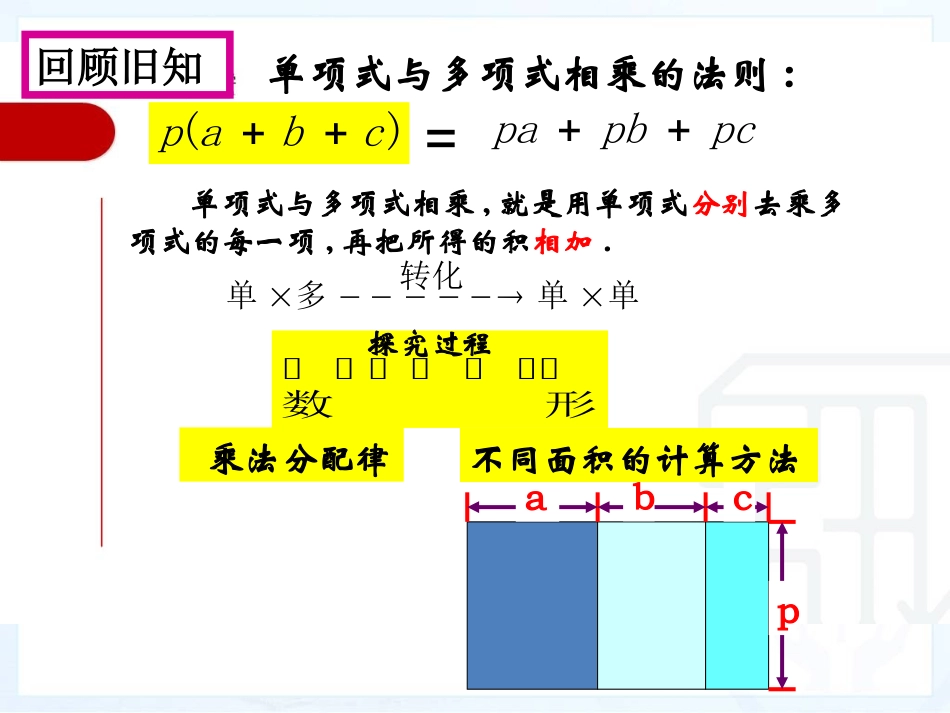
14.1.4整式的乘法多项式乘以多项式cbap)(cbappcpbpa=单单转化多单单项式与多项式相乘的法则:单项式与多项式相乘,就是用单项式分别去乘多项式的每一项,再把所得的积相加.乘法分配律形数不同面积的计算方法回顾旧知探究过程引例:为了扩大街心花园的绿地面积,有一块原长a米,宽为p米的长方形绿地增长了b米,加宽了q米,你能表示出扩大后的绿地面积吗?abpq法则cbap)(cbappcpbpa=单单转化多单单项式与多项式相乘的法则:单项式与多项式相乘,就是用单项式分别去乘多项式的每一项,再把所得的积相加.乘法分配律不同面积的计算方法形数探究过程pcpbpacbap)(单项式与多项式相乘,就是用单项式分别去乘多项式的每一项,再把所得的积相加.bqbpaqapqpba))((多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.你能类比单项式与多项式相乘的法则,叙述多项式与多项式相乘的法则吗?总结拓展提高1、已知(x+a)(x-4)=x2-x-12,则a=_____2、多项式(my+8)(2-3y)的计算结果不含y项,则m=_____(1)本节课学习了哪些主要内容?(2)在运用多项式与多项式相乘的法则时,你认为应该注意哪些问题?(3)我们在探索多项式与多项式相乘的法则的过程中,运用了哪些思想方法?课堂小结整体思想方法1利用长方形面积的计算数形结合方法2(a+b)(p+q)=(a+b)·p+(a+b)·q=ap+bp+aq+bq.即把(a+b)看成一个整体,用分配律(a+b)(p+q)=ap+aq+bp+bq转化思想类比方法