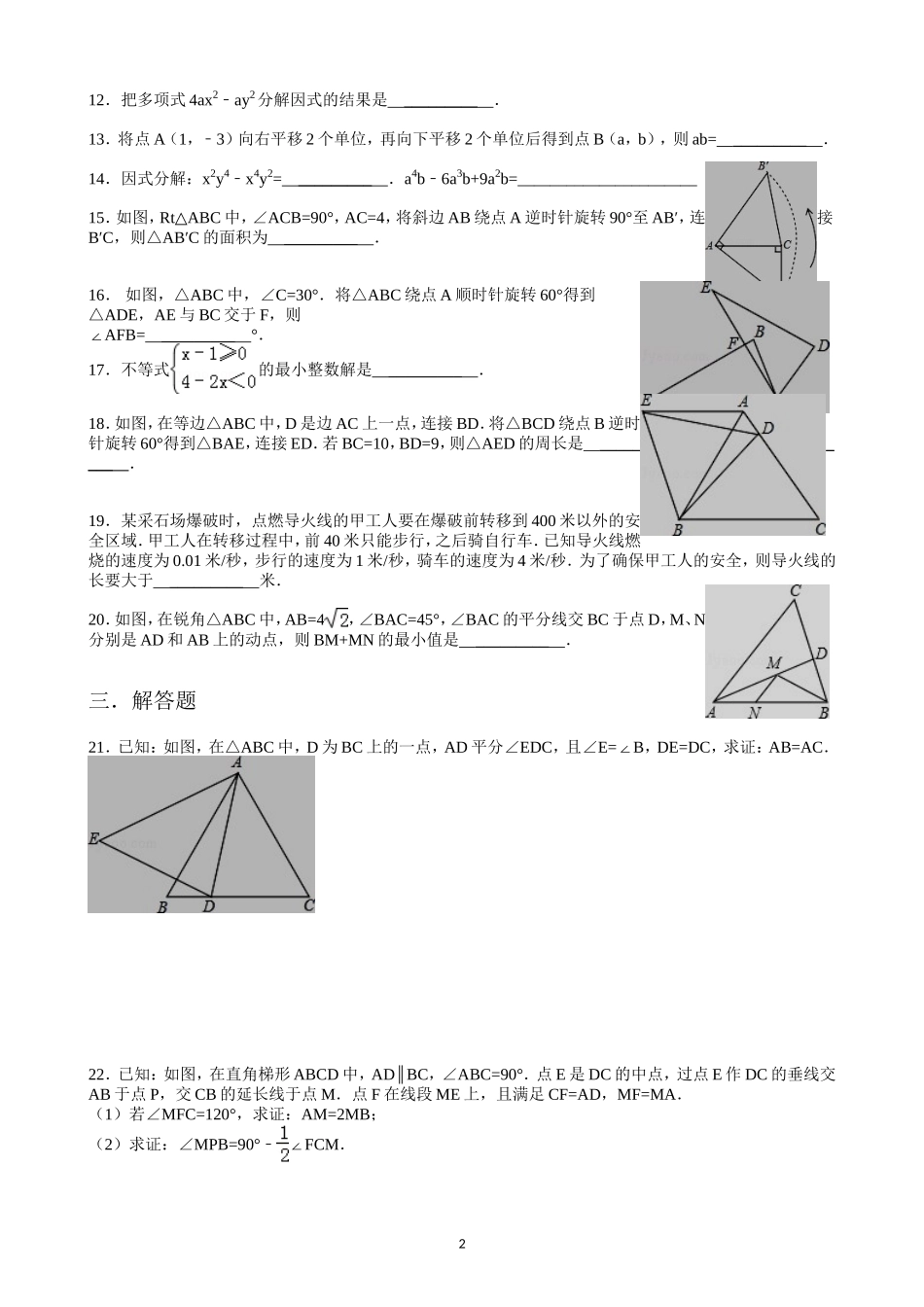
期中模拟题一.选择题1.等腰三角形一腰上的高与另一腰的夹角为30°,则顶角的度数为()A.60°B.120°C.60°或150°D.60°或120°2.如图,△ABC中,AB=AC,AD=DE,∠BAD=20°,∠EDC=10°,则∠DAE的度数为()A.30°B.40°C.60°D.80°3.如图,在△ABC中ADBC⊥,CEAB⊥,垂足分别为D、E,AD、CE交于点H,已知EH=EB=3,AE=4,则CH的长是()A.1B.2C.3D.44.如图,RtABC△中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为()A.2B.2.5或3.5C.3.5或4.5D.2或3.5或4.55.不等式x5﹣>4x1﹣的最大整数解是()A.2﹣B.1﹣C.0D.16.不等式组的解集在数轴上表示为()A.B.C.D.7.下列四个图形中,是中心对称图形的是()A.B.C.D.8.如图,将△ABC绕点A逆时针旋转一定角度,得到△ADE.若∠CAE=65°,∠E=70°,且ADBC⊥,∠BAC的度数为()A.60°B.75°C.85°D.90°9.如图,OAOB⊥,等腰直角三角形CDE的腰CD在OB上,∠ECD=45°,将三角形CDE绕点C逆时针旋转75°,点E的对应点N恰好落在OA上,则的值为()A.B.C.D.10.下列分解因式正确的是()A.3x26x=x﹣(3x6﹣)B.a﹣2+b2=(b+a)(ba﹣)C.4x2y﹣2=(4x+y)(4xy﹣)D.4x22xy+y﹣2=(2xy﹣)2二.填空题11.如图,在等边△ABC中,AB=6,D是BC的中点,将△ABD绕点A旋转后得到△ACE,那么线段DE的长度为_________.112.把多项式4ax2ay﹣2分解因式的结果是_________.13.将点A(1,﹣3)向右平移2个单位,再向下平移2个单位后得到点B(a,b),则ab=_________.14.因式分解:x2y4x﹣4y2=_________.a4b6a﹣3b+9a2b=______________________15.如图,RtABC△中,∠ACB=90°,AC=4,将斜边AB绕点A逆时针旋转90°至AB′,连接B′C,则△AB′C的面积为_________.16.如图,△ABC中,∠C=30°.将△ABC绕点A顺时针旋转60°得到△ADE,AE与BC交于F,则AFB=∠_________°.17.不等式的最小整数解是_________.18.如图,在等边△ABC中,D是边AC上一点,连接BD.将△BCD绕点B逆时针旋转60°得到△BAE,连接ED.若BC=10,BD=9,则△AED的周长是_________.19.某采石场爆破时,点燃导火线的甲工人要在爆破前转移到400米以外的安全区域.甲工人在转移过程中,前40米只能步行,之后骑自行车.已知导火线燃烧的速度为0.01米/秒,步行的速度为1米/秒,骑车的速度为4米/秒.为了确保甲工人的安全,则导火线的长要大于_________米.20.如图,在锐角△ABC中,AB=4,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是_________.三.解答题21.已知:如图,在△ABC中,D为BC上的一点,AD平分∠EDC,且∠E=B∠,DE=DC,求证:AB=AC.22.已知:如图,在直角梯形ABCD中,ADBC∥,∠ABC=90°.点E是DC的中点,过点E作DC的垂线交AB于点P,交CB的延长线于点M.点F在线段ME上,且满足CF=AD,MF=MA.(1)若∠MFC=120°,求证:AM=2MB;(2)求证:∠MPB=90°﹣FCM∠.223.端午节期间,某校“慈善小组”筹集到1240元善款,全部用于购买水果和粽子,然后到福利院送给老人,决定购买大枣粽子和普通粽子共20盒,剩下的钱用于购买水果,要求购买水果的钱数不少于180元但不超过240元.已知大枣粽子比普通粽子每盒贵15元,若用300元恰好可以买到2盒大枣粽子和4盒普通粽子.(1)请求出两种口味的粽子每盒的价格;(2)设买大枣粽子x盒,买水果共用了w元.①请求出w关于x的函数关系式;②求出购买两种粽子的可能方案,并说明哪一种方案使购买水果的钱数最多.24.将△ABC绕点B逆时针旋转α得到△DBE,DE的延长线与AC相交于点F,连接DA、BF.(1)如图1,若∠ABC=α=60°,BF=AF.①求证:DABC∥;②猜想线段DF、AF的数量关系,并证明你的猜想;25.解不等式(组).把解集在数轴上表示出来.(1).(2)3(3)(4)26.已知,如图,在RtABC△中,∠ACB=90°,∠A=30°,CDAB⊥交AB于点E,且CD=AC,DFBC∥,分别与AB、AC交于点G、F.(1)求证:GE=GF;(2)若BD=1,求DF的长.4