平方差公式-(2)VIP免费

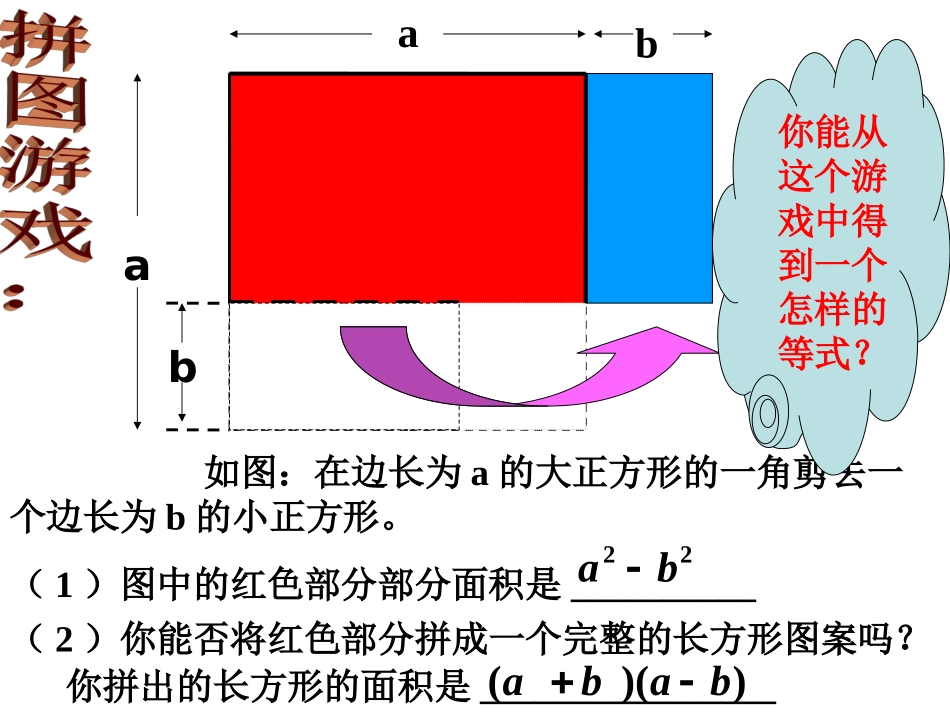
8.58.5乘法公式乘法公式遵化市第三中学马石新abab如图：在边长为a的大正方形的一角剪去一个边长为b的小正方形。（1）图中的红色部分部分面积是__________22ba（2）你能否将红色部分拼成一个完整的长方形图案吗？))((baba你能从这个游戏中得到一个怎样的等式？你拼出的长方形的面积是________________学习目标：1、会推导平方差公式，并了解几何背景。2、掌握公式并会运用它进行计算。3、经历探索公式的过程，进一步感受数与形的关系，感悟数形结合的思想。二、平方差公式两个数的和与这两个数的差的积等于两个数的和与这两个数的差的积等于这两个数的平方差．这两个数的平方差．22bababa22))((bababababa22ba知识出击:概念挖掘:25/2/14例题1•(2x+y)(2x-y)(x+5y)(x-5y)•(-5a+3b)(-5a-3b)(1)(1)(a+b)((a+b)(aa−−b)b)；；(2)(2)(a(a−−b)(bb)(b−−a);a);(3)(3)(a+2b)(2b+a);(a+2b)(2b+a);(4)(4)(a(a−−b)(a+b);b)(a+b);(5)(5)((2x+y)(y2x+y)(y−−2x).2x).((不能不能))1.1.下列式子可用平方差公式计算吗下列式子可用平方差公式计算吗??为什么为什么??如果能如果能够，怎样计算够，怎样计算??((不能不能))((不能不能))((能能))−−((aa22−−bb22))==−−aa22++bb22;;((不能不能))检验成果:随堂练习(1)(1)((aa++33)()(aa−−33))；；(2)(2)(2(2aa++33bb)(2)(2aa−−33bb));;22、、计算：计算：(3)(3)(1+2c)(1-2c)..例例22利用平方差公式计算：利用平方差公式计算：1998×20021998×2002；；3、灵活应用公式（1）解：1998×2002原式=（2000－2）（2000+2）=20002－22=4000000-4=3999996王敏捷同学去商店王敏捷同学去商店买了单价是买了单价是9.89.8元元//千克的糖果千克的糖果10.210.2千克，千克，售货员刚拿起计算器，王敏捷就说出应付售货员刚拿起计算器，王敏捷就说出应付99.9699.96元，元，结果与售货员计算出的结果相吻合。结果与售货员计算出的结果相吻合。售货员很惊讶地说：售货员很惊讶地说：““你好象是个神童，怎么算得这么快？”你好象是个神童，怎么算得这么快？”王敏捷同学说王敏捷同学说：：““过奖了，我利用了在数学上刚学过的一个公式。”过奖了，我利用了在数学上刚学过的一个公式。”你知道王敏捷同学用的是一个什么样的公式吗？你知道王敏捷同学用的是一个什么样的公式吗？怎么计算的吗怎么计算的吗??随堂练习挑战自我挑战自我例题：街心花园有一块边长为a米的正方形草坪，经统一规划后，南北向要加长2米，而东西向要缩短2米，问改造后的长方形草坪的面积是多少？解：(a+2)(a-2)=（a2-4）平方米答：改造后的长方形草坪的面积是（a2-4）平方米试用语言表述平方差公式试用语言表述平方差公式((aa++bb)()(aa−−bb))==aa22−−bb22。。应用平方差公式时要注意一些什么？应用平方差公式时要注意一些什么？两数和与两数和与这这两数差的积，等于它们的平方差。两数差的积，等于它们的平方差。拓展练习运用平方差公式计算：运用平方差公式计算：((44aa1)(41)(4aa1)1)．．((用两种方法用两种方法))运用平方差公式时，运用平方差公式时，要紧扣公式的特征，要紧扣公式的特征，找出相等的“项”和符号相反的“项”，然后应用公式．找出相等的“项”和符号相反的“项”，然后应用公式．法一法一利用加法交换律，利用加法交换律，变成公式标准形式。变成公式标准形式。((44aa−−1)(41)(4aa−−1)1)====((1)1)22−−(4(4aa))22==11−−1616aa22。。法二法二提取两“提取两“−−”号中的“”号中的“−−”号，”号，变成公式标准形式变成公式标准形式。。((44aa−−1)1)(4(4aa−−1)1)==(4(4aa++1)1)((44aa−−1)1)(4(4aa−−1)1)==(4(4aa))22−−11计算计算时千万别忘了你提出的“时千万别忘了你提出的“”号、”号、添括号；添括号；注意注意[][]==11−−1616aa22。。((44aa−−1)(41)(4aa−−1)1)−−11−−44aa−−11++44aa11、判断正误，并改正、判断正误，并改正(1)(-m-2n)(m-2n)=(1)(-m-2n)(m-2n)=(2)(-a+b)(-a-b)=(2)(-a+b)(-a-b)=22、计算、计算（（11））(x-2)(x+2)(x-2)(x+2)（（22））(3m+2n)(3m-2n)(3m+2n)(3m-2n)（（33））(3a-4b)(-4b-3a)(3a-4b)(-4b-3a)（（44））99×10199×101222nm22-ba课堂检测课外练习: