整式的乘除-(2)VIP免费

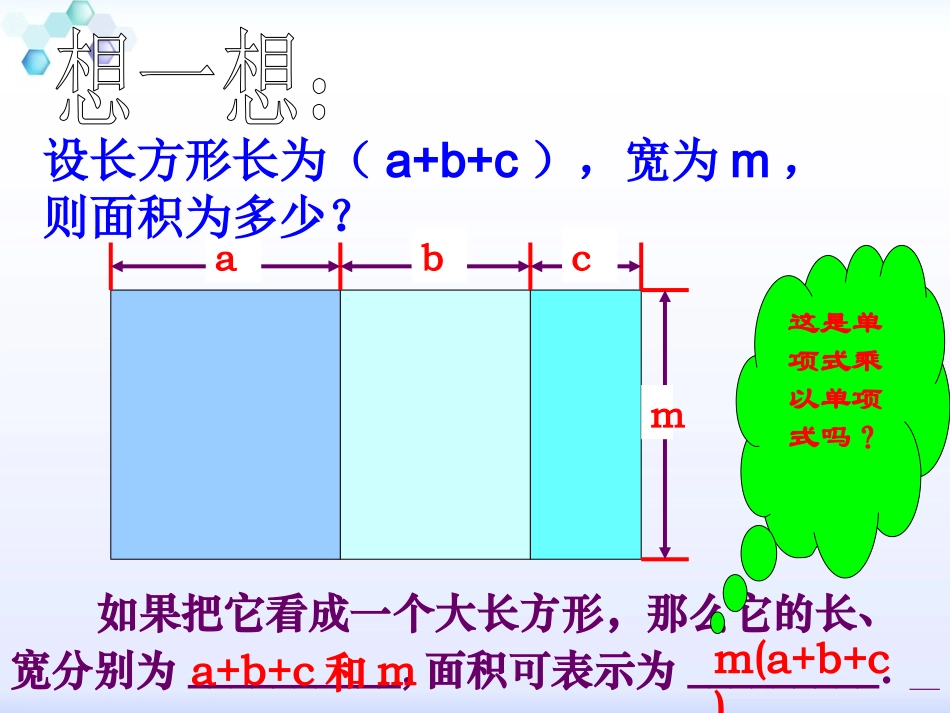
第第1414章整式乘除与因式分解章整式乘除与因式分解复习提问：1.请说出单项式与单项式相乘的法则：单项式与单项式相乘，把它们的单项式与单项式相乘，把它们的系数系数、、相同字母相同字母分别分别相乘，相乘，对于对于只只在在一个一个单项式单项式里里含含有的有的字母字母，则连同它的，则连同它的指数指数作作为为积积的一个的一个因式因式。。计算：yxxyyxx32332)()2()2())(1(23322)()()(21)(2)2(abcabcbcabcacbam设长方形长为（a+b+c），宽为m，则面积为多少？如果把它看成一个大长方形，那么它的长、宽分别为__________,面积可表示为_________.a+b+c和mm(a+b+c)这是单项式乘以单项式吗？如果把它看成三个小长方形，那么它们的面积可分别表示为_____、_____、_____.mmabmcmamcmb想一想：还有其它方法计算吗？如果把它看成三个小长方形，那么它们的面积可分别表示为_____、_____、_____.如果把它看成一个大长方形，那么它的面积可表示为_________.cbammamcmbm(a+b+c)ma+mb+mcm(a+b+c))(cbammcmbma=你能用你能用所学的知识所学的知识解释这个等式吗？解释这个等式吗？mm((aa++b+cb+c)=)=mamambmbmcmc++++2a2a22((33aa22-5-5bb)=)=2a2a2.2.3a3a222a2a2.2.(-5b)(-5b)++==6a6a44-10a-10a22bb类似的:单项式与多项式相乘乘法分配律单项式与多项式相乘,就是用单项式分别去乘多项式的每一项,再把所得的积相加.单项式与多项式相乘的法则:八年级数学第十五章整式的乘法自主探究计算：例)35(2)1(22baabab;21)232)(2(2ababab单项式与多项式相乘时，分两个阶段：单项式与多项式相乘时，分两个阶段：①①按乘法分配律把乘积写成单项式与单项按乘法分配律把乘积写成单项式与单项式乘积的代数和的形式；式乘积的代数和的形式；②②单项式的乘法运算。单项式的乘法运算。几点注意：几点注意：1.1.单项式乘多项式的结果仍是多项式，单项式乘多项式的结果仍是多项式，积的项数与原多项式的项数相同。积的项数与原多项式的项数相同。2.2.在单项式乘法运算中要注意系数的符在单项式乘法运算中要注意系数的符号。号。3.3.不要出现漏乘现象，运算要有顺序。不要出现漏乘现象，运算要有顺序。巩固法则练习2计算下列各式：（1）（2）（3）（4）352-aab（）；36--xyx（）（）；2523xxx（-4）；222+.aaabb（-）（-）15a2-6ab.-6x2+18xy.10x3-20x2+15x.2a3+2a2b-2ab2.计算结果中，如果有同类项，记住要合并哟巩固法则例2化简：2221-++.xxxxx（）（）解：原式=x3-x2+2x3+2x2=3x3+x2.3.化简：x(x2-1)+2x2(x+1)-3x(2x-5).【解析】原式=x3-x+2x3+2x2-6x2+15x=3x3-4x2+14x.巩固法则练习3化简：（1）（2）221223-+-+xxxxx（）（）；21313222+--.xxxx（）（）解：（1）原式=x3-x2+2x3-4x2+6x=3x3-5x2+6x.23321991x+x-x+6x=-x+x+7x.2222（2）的值求1.已知)(63522babbaabab解：原式=a3b6-a2b4-ab2=(ab2)3-(ab2)2-ab2∵ab2=-6∴原式=（-6）3-（-6）2-（-6）=-216-36+6=-246先化简再求值:.251)5()1(2322xxxxxxxx，其中深入探索----算一算单项式与多项式相乘八年级数学第十四章整式的乘法xxxxxxx5234234解：原式时当251x512515原式x57x-(x–3)x–3x(2–x)=(2x+1)x+6解：去括号，得7x–x2+3x–6x+3x2=2x2+x+6移项，得7x–x2+3x–6x+3x2-2x2-x=6合并同类项，得3x=6系数化为1，得x=2解方程深入探索----解一解单项式与多项式相乘八年级数学第十四章整式的乘法（1）本节课学习了哪些主要内容？（2）在运用单项式与多项式相乘的法则时，你认为应该注意哪些问题？（3）探索单项式与多项式相乘的法则的过程，体现了哪些思想方法？课堂小结作业：•课本P149第4、6题•每课必练：P63-64页。Thankyou!