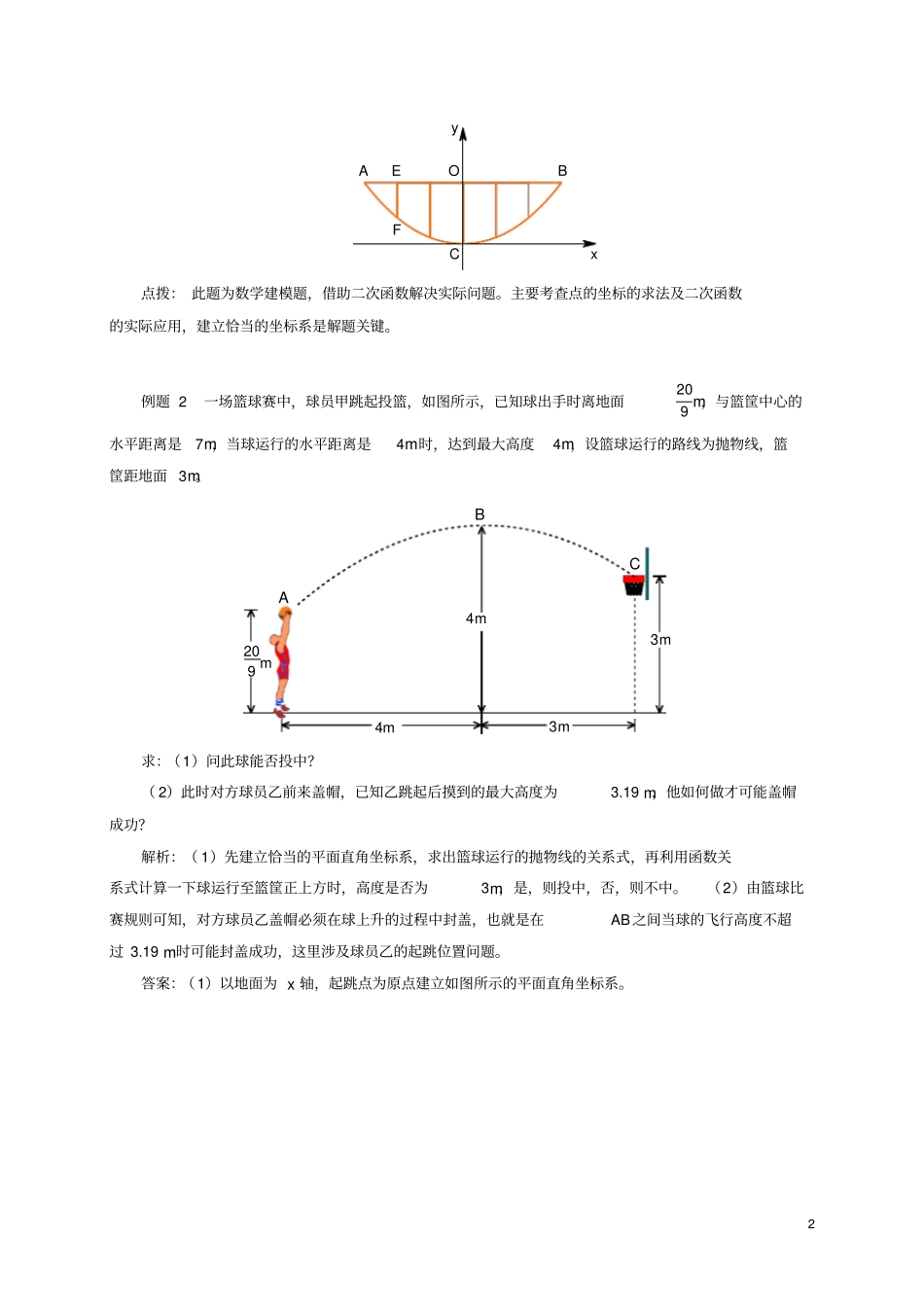
建立适当的坐标系解决实际问题一、建立坐标系解决实际问题的一般步骤1.恰当地建立直角坐标系;2.将已知条件转化为点的坐标;3.合理地设出所求函数关系式;4.代入已知条件或点的坐标,求出关系式;5.利用关系式求解问题。方法归纳:(1)恰当地建立直角坐标系是准确、简捷地求解问题的关键;(2)将已知条件转化为点的坐标时,应注意距离与坐标的关系;(3)设函数关系式应根据题设合理选择三种函数式中的一种;(4)求解问题应能将点的坐标正确地转化为距离或高度。总结:1.能分析实际问题中数量关系,建立二次函数模型。2.能够建立坐标系,确定二次函数关系式,并解决实际问题。例题1如图,某校的围墙由一段相同的凹曲拱组成,其拱状图形为抛物线的一部分,栅栏的跨径AB之间按相同间隔0.2米用5根立柱加固,拱高OC为0.36米,则立柱EF的长为()ABCEFOA.0.4米B.0.16米C.0.2米D.0.24米解析:由于按相同的间距0.2m用5根立柱加固,则AB=0.2×6=1.2,以C为坐标系的原点,OC所在直线为y轴建立坐标系,由此得到抛物线过B(0.6,0.36)、C(0,0)、A(-0.6,0.36),据此求出其解析式。把x=-0.4代入后求出y,令EF=0.36-y即可。答案:如图,以C为坐标系的原点,OC所在直线为y轴建立坐标系,设抛物线解析式为y=ax2,由题意知,图象过B(0.6,0.36),代入得:0.36=0.36a,∴a=1,即y=x2。 F点横坐标为-0.4,∴当x=-0.4时,y=0.16,∴EF=0.36-0.16=0.2米。故选C。2ABCEFOxy点拨:此题为数学建模题,借助二次函数解决实际问题。主要考查点的坐标的求法及二次函数的实际应用,建立恰当的坐标系是解题关键。例题2一场篮球赛中,球员甲跳起投篮,如图所示,已知球出手时离地面209m,与篮筐中心的水平距离是7m,当球运行的水平距离是4m时,达到最大高度4m,设篮球运行的路线为抛物线,篮筐距地面3m。209m3m3m4m4mABC求:(1)问此球能否投中?(2)此时对方球员乙前来盖帽,已知乙跳起后摸到的最大高度为3.19m,他如何做才可能盖帽成功?解析:(1)先建立恰当的平面直角坐标系,求出篮球运行的抛物线的关系式,再利用函数关系式计算一下球运行至篮筐正上方时,高度是否为3m,是,则投中,否,则不中。(2)由篮球比赛规则可知,对方球员乙盖帽必须在球上升的过程中封盖,也就是在AB之间当球的飞行高度不超过3.19m时可能封盖成功,这里涉及球员乙的起跳位置问题。答案:(1)以地面为x轴,起跳点为原点建立如图所示的平面直角坐标系。3ABCOxy由题意知,抛物线顶点坐标为(4,4),经过(0,209)。设抛物线的关系式为y=a(x-4)2+4,把x=0,y=209代入,得209=a(0-4)2+4,∴a=-19。∴y=-19(x-4)2+4,即y=-19x2+89x+209。当x=7时,y=-19(7-4)2+4=3,而篮筐中心距地面刚好是3m,∴此球能够投中。(2)当y=3.19时,-19(x-4)2+4=3.19,解得x1=1.3,x2=6.7。由于篮球比赛规则规定盖帽必须在球上升过程中,当x=1.3时上升,当x=6.7时下降。所以,球员乙必须在球员甲前1.3m之内跳起封盖才可能成功。点拨:本例通过建立平面直角坐标系求出二次函数的关系式,再利用二次函数的有关性质来解决实际问题,将实际问题转化为数学模型是关键,而利用数学知识去解决实际问题时还要注意符合实际意义。有些实际问题中并没有明确给出它符合哪一种函数,这时应根据题目提供的数据画出图象,根据图象判断函数的种类。若所给数据符合二次函数特征,可选取三组数据(即三点)求出二次函数的关系,但必须将其他点代入验证,这一步不可少,只有验证无误后方可认定是二次函数,以防错误判断。例行驶中的汽车,在刹车后由于惯性的作用,还要继续向前滑行一段距离才能停止,这段距4离称为“刹车距离”。为了测定某型号汽车的刹车性能(车速不能超过140km/h),对这种汽车进行测试,测得数据如下:刹车时车速(km/h)0102030405060刹车距离(m)00.31.02.13.65.57.8(1)以车速为x轴,以刹车距离为y轴,在坐标系中描出这些数据所表示的点,并用平滑的曲线联结这些点,得到函数的大致图象;(2)观察图象,估计函数的类型;(3)如果该函数解析式为y=0.002x2+0.01x,...