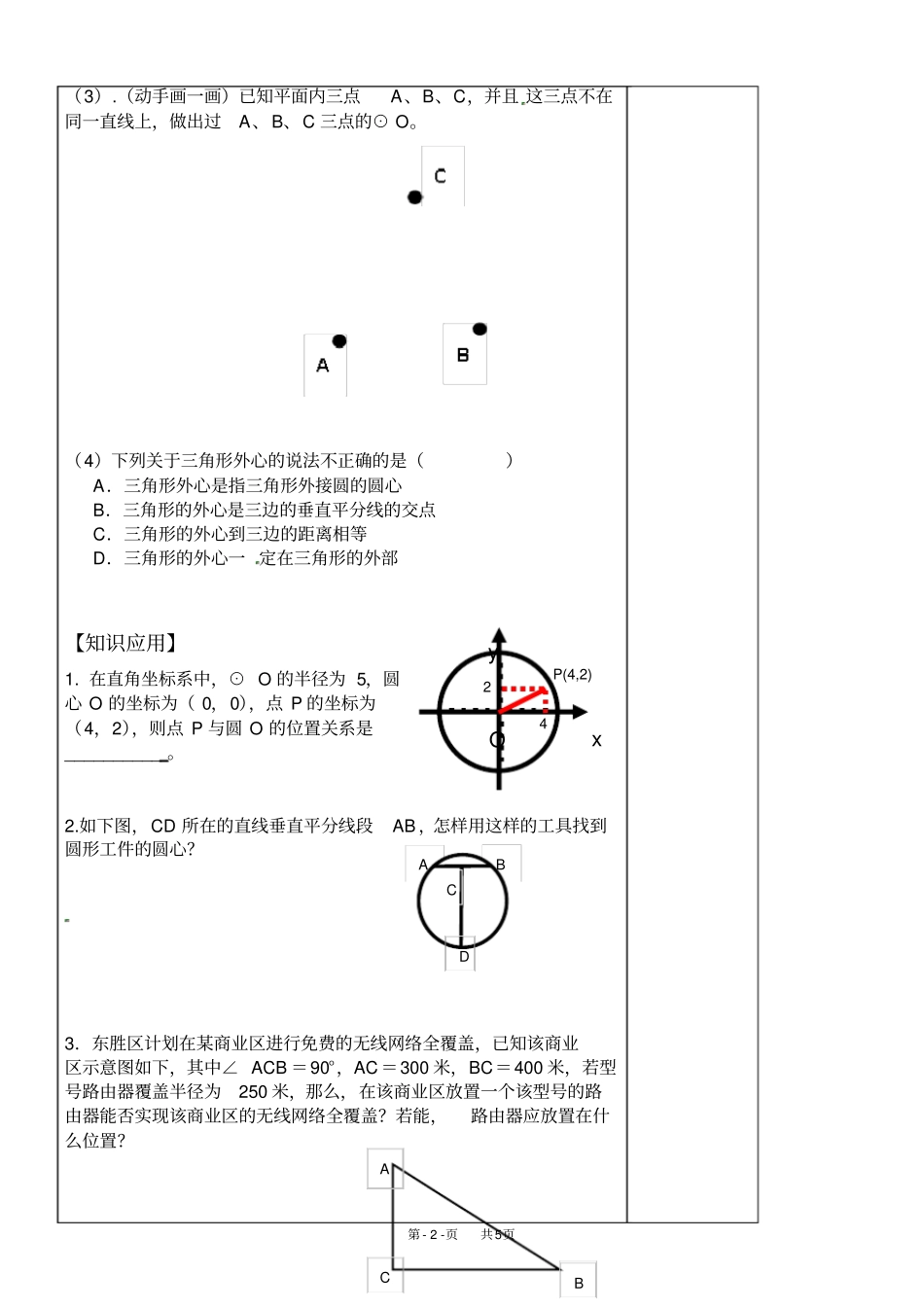
第-1-页共5页科目数学课型新授课级九级印刷时间主备梁小敏同伴李庆丰组长签字授课时间目标导航学习目标1.了解点和圆的位置关系及不在同一直线三点确定一个圆的事实2.培养学生数形转化的能力,学会归纳、类比.学习重点点和圆的位置关系.学习难点不在同一直线的三点确定一个圆学习过程备注【引入新课】爱好运动的小华、小强、小兵三人相邀搞一次掷飞镖比赛。他们把靶子钉在一面土墙上,规则是谁掷出落点离红心越近,谁就胜。如下图中A、B、C三点分别是他们三人某一轮掷镖的落点,你认为这一轮中谁的成绩好?解决这个问题要研究点和圆的位置关系。【学习内容】要求:1.带着导引中的问题自学课本的内容并尝试完成自学检测.然后在组内交流学习所获。1.自学导引(1)平面内点和圆的位置关系有几种?如何判断?(2)平面内确定一个圆至少需要几点?这几个点要满足什么条件?为什么?(3)经过同一条直线上的三点能作出一个圆吗?教材上是如何决这一问题的?对于种方法你了解多少?2.自学检测:(1)已知⊙O的半径为8cm,平面内有一点A,若OA=12cm,则可知点A在⊙O的。(2)平面内有三点A、B、C和⊙O,⊙O的半径为6cm,如果点A在⊙O内,则OA的取值范围是,如果点B在⊙O上,则OB的取值范围是,如果点C在⊙O外,则OC的取值范围是,ABCO第-2-页共5页(3).(动手画一画)已知平面内三点A、B、C,并且这三点不在同一直线上,做出过A、B、C三点的⊙O。(4)下列关于三角形外心的说法不正确的是()A.三角形外心是指三角形外接圆的圆心B.三角形的外心是三边的垂直平分线的交点C.三角形的外心到三边的距离相等D.三角形的外心一定在三角形的外部【知识应用】1.在直角坐标系中,⊙O的半径为5,圆心O的坐标为(0,0),点P的坐标为(4,2),则点P与圆O的位置关系是__________。2.如下图,CD所在的直线垂直平分线段AB,怎样用这样的工具找到圆形工件的圆心?3.东胜区计划在某商业区进行免费的无线网络全覆盖,已知该商业区示意图如下,其中∠ACB=90°,AC=300米,BC=400米,若型号路由器覆盖半径为250米,那么,在该商业区放置一个该型号的路由器能否实现该商业区的无线网络全覆盖?若能,路由器应放置在什么位置?P(4,2)42xyOBACDABC第-3-页共5页【拓展延伸】我们已经知道任意一个三角形一定有一个外接圆,那么对于一个任意四边形是否也有外接圆呢?1.我们先从特殊的四边形研究起,想一想,下列四边形是否一定有外接圆呢?(1)平行四边形(2)矩形(3)菱形(4)正方形2.对(1)中的结论进行总结,想一想,一个四边形具备怎样的条件时,这个四边形一定有外接圆。【课堂检测】要求:独立完成下列各题.日期班级姓名整洁分数1.⊙O的半径10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:点A在;点B在;点C在。2.在同一平面上,⊙O外一点P到⊙O上一点的距离为最长为6cm,最短为5cm,则⊙O的半径为。3.如图,某海域点A处周围3km的圆形区域为多暗礁的危险区,但水生物资源丰富,渔船要从B处前进到A处进行捕鱼作业,B、A之间的距离是10km。如果渔船始终保持10km/h的航速,那么在什么时段内,渔船是安全的?渔船何时进入危险区域?C第-4-页共5页第-5-页共5页