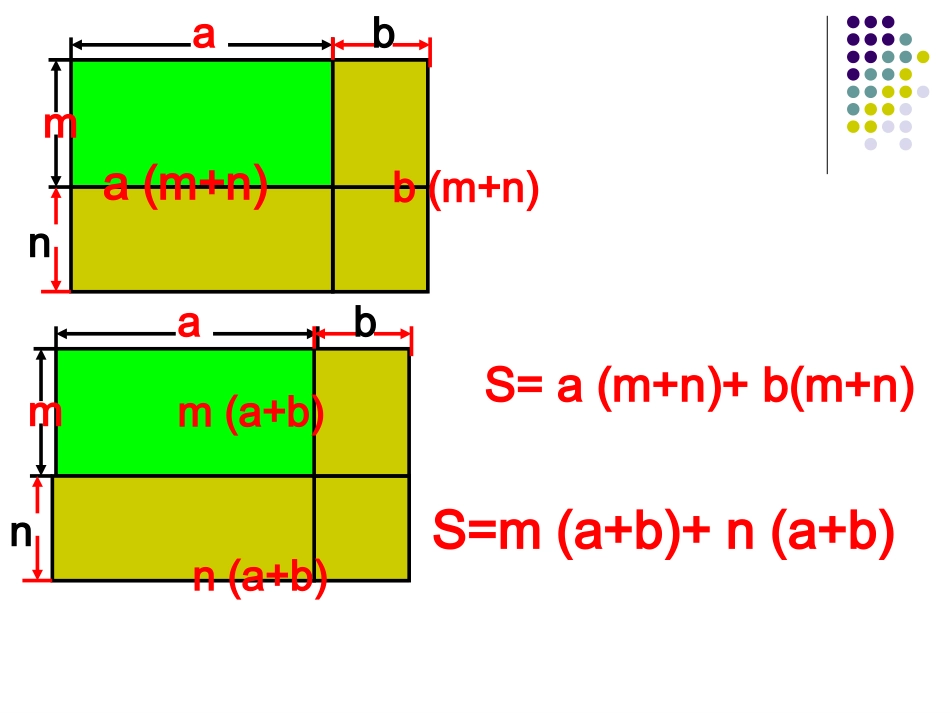
多项式乘以多项式多项式乘以多项式将原有的长为a米,宽为m米的长方形绿地加长b米,加宽n米,扩建成为美化校园绿草地。你能用几种方法计算扩展后绿地的面积?长为(a+b),宽为(m+n)S=(a+b)(m+n)manbS=am+an+bm+bn(a+b)(m+n)=am+an+bm+bnambmanbnmanbmanba(m+n)b(m+n)m(a+b)n(a+b)S=a(m+n)+b(m+n)S=m(a+b)+n(a+b)方案一:S=am+an+bm+bnabmn方案二:方案二:S=a(m+n)+b(m+n)S=a(m+n)+b(m+n)方案三方案三:S=m(a+b)+n(a+b):S=m(a+b)+n(a+b)方案四方案四:S=(a+b)(m+n):S=(a+b)(m+n)∴(a+b)(m+n)=a(m+n)+b(m+n)=am+an+bm+bn观察上述式子,你能得到(x-3)(x-6)的结果吗?或(a+b)(m+n)=m(a+b)+n(a+b)=am+bm+an+bn(x–3)(y–6)=x(y–6)–3(y–6)=xy–6x–3y+18∵∵四种方案算出的面积相等四种方案算出的面积相等归纳得出:多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.(a+b)(m+n)=am+an+bm+bn(a+b)=a+b(a+b)=a+b=am+an+bm+bn=am+an+bm+bn(m+n)(m+n)(m+n)(m+n)(m+n)(m+n)解:(1)原式=3x·x–3x·2+1·x–1×2(2)原式=x·x–x·y–8y·x+8y·y=3x2–6x+x–2=3x2–5x–2=x2–xy–8xy+8y2=x2–9xy+8y2(1)(3x+1)(x–2)(2)(x–8y)(x–y)例6计算(1)(2x+1)(x+3)(2)(m+2n)(m–3n)(3)(a-1)2(4)(a+3b)(a–3b)答案:(1)2x2+7x+3;(2)m2––mn––6n2;(3)a2-2a+1;(4)a2-9b2(5)(x+2)(x+3)(6)(x-4)(x+1)(7)(y+4)(y-2)(8)(y-5)(y-3)(5)x2+5x+6;(6)x2-3x-4;(7)y2+2y-8;(8)y2-8y+15.检测一(3)化简x(4x–y)–(2x+y)(2x–y)(1)(x–y)2(2)例例(x+y)(x2–xy+y2)解:(1)原式=(x–y)(x–y)=x2–xy–xy+y2=x2–2xy+y2(2)原式=x3–x2y+xy2+yx2–xy2+y3=x3+y3(3)原式=4x2–xy–(4x2–2xy+2xy–y2)=4x2–xy–4x2+y2=–xy+y2(x+2)(x+3)(x+2)(x+3)==xx22+5x+6;+5x+6;(x-4)(x+1)=(x-4)(x+1)=xx22–3x–3x--44(y+4)(y-2)=(y+4)(y-2)=yy22+2y+2y--88(y-5)(y-3)(y-5)(y-3)==yy22--8y+158y+15观察上述式子,你可以得出一个什么规律吗?(x+p)(x+q)=x2+(p+q)x+pq(1)(x+4)(x+9)=x(1)(x+4)(x+9)=x22+mx+36+mx+36(2)(x-2)(x-18)=x²+mx+36(2)(x-2)(x-18)=x²+mx+36(3)(x+3)(x+p)=x²+mx+36(3)(x+3)(x+p)=x²+mx+36(4)(x-6)(x-p)=x²+mx+36(4)(x-6)(x-p)=x²+mx+36(5)(x+p)(x+q)=x²+mx+36(5)(x+p)(x+q)=x²+mx+36(p(p,,qq为正整数为正整数))(1)m=13(2)m=-20(3)p=12,m=15(4)p=6,m=-12(5)p=4,q=9,m=13p=2,q=18,m=20p=3,q=12,m=15p=6,q=6,m=12先化简再求值:解:原式=a3=a2(a-1)-(a2-1)(2++a),其中a=原式=-3×()2+()+2212121-a22a2++a3当a=,––()-2-aa3-a2-2a2-a3++2+a=-3a2+a+2如果a2+a=1,那么求(a-5)(a+6)的值若(x+m)(x-2)的积中不含关于x的一次项,求m的值拓展延伸小结1、多项式与多项式相乘多项式与多项式相乘,,先用一个多项式先用一个多项式的每一项乘另一个多项式的每一项的每一项乘另一个多项式的每一项,,再把所再把所得的积相加得的积相加..(a+b)(m+n)=am+an+bm+bn2、多项式与多项式相乘时,多项式的每一项都应该带上它前面的正负号。多项式是单项式的和,每一项都包括前面的符号,在计算时一定要注意确定各项的符号。4、在数学知识的学习中,“转化”思想是的重要思想方法。在今天的学习中,第一步是“转化”为多项式与单项式相乘,第二步是“转化”为单项式乘法。即将新的知识、方法化为已知的数学知识、方法。从而使学习能够进行。3、(x+p)(x+q)=x2+(p+q)x+pq作业:1.暗线:课本P10542.《南》:P59-P60