实数复习课件VIP免费

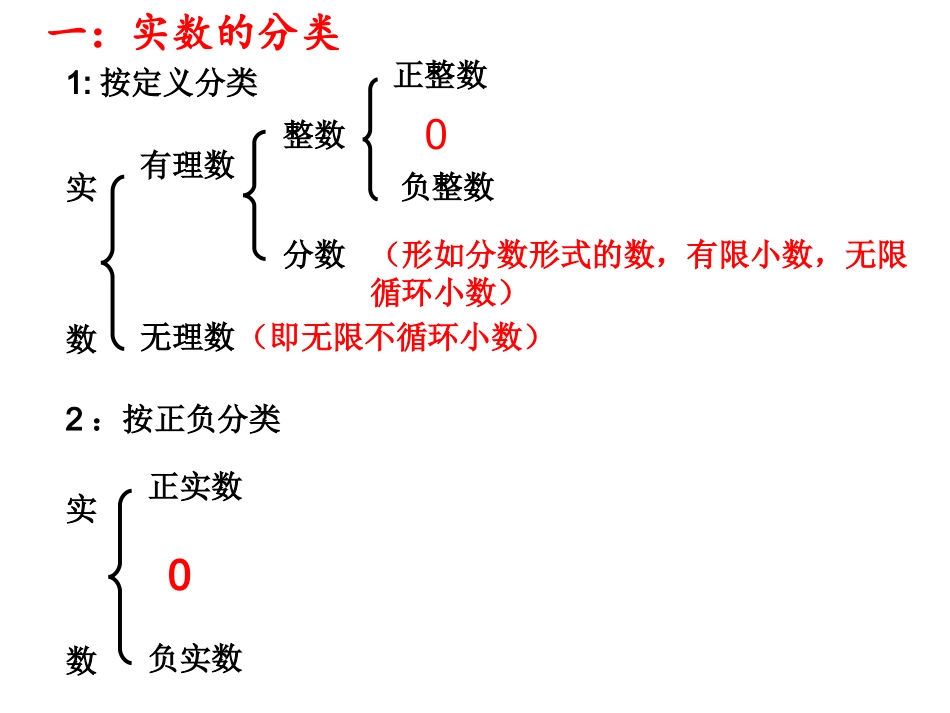
一：实数的分类1:按定义分类实数有理数无理数整数分数正整数负整数0（即无限不循环小数）（形如分数形式的数，有限小数，无限循环小数）2：按正负分类实数正实数0负实数1：在实数－，，0，，，－3.14，0.1010010001…（每两个1之间依次多1个0），sin30°这8个实数中，无理数有（）A．1个B．2个C．3个D．4个23324二：实数的相关概念数轴，相反数，绝对值，倒数，算术平方根，平方根，立方根1：数轴上的数有什么性质？原点左边的为负数，原点右边的为正数原点右边的数大于原点左边的数a0.实数在数轴上对应的点如图所示，则a，-a，-1的大小关系是（）A．B．C．D．1aaaaa1aa1aa-12：只有————不同的两个数互为相反数符号a的相反数为-a若a和b互为相反数，则a+b=03：绝对值的定义：数轴上表示这个数的点离原点的距离正数，负数，零的绝对值分别是什么数？和它本身有什么关系？任意实数的绝对值都是非负数即︱a︳≥0︱a︳(a＞0)(a=0)(a＜0)=a=0=-a(1):在实数0，1，，0.1235中，无理数的个数为（）A.0个B.1个C.2个D.3个(3):已知实数在数轴上的位置如图所示，则化简的结果为（）A．1B．C．D．2|1|aa10a112a21a(2):的相反数是__=______．14134:判断：任何实数都有倒数0没有倒数若两个数的乘积为1，则称这两个数互为倒数。若a,b互为倒数，则ab=1求下列数的倒数：-5，-0.75，-，,233235：平方根（1）任何数都有平方根吗？平方根如何表示？（2）正数有几个平方根？这两个根之间有什么关系？正数和0才有平方根，当a≥0时，a的平方根记作±a正数有两个平方根，且这两个根互为相反数4的平方根是（）A．±2B．2C．±D．若-6是m的一个平方根，则m=已知与是m的平方根，求m的值12a5a6:算术平方根(即平方根中的那个正的根）正数和0才有算术平方根，当a≥0时，a的算术平方根记作a正数和0的算术平方根均只有一个a≥07：常见的非负数有：22340abc，cba．若则几个非负数的和为0，则它们必须同时为08:形如（a≥0)的式子，我们称之为二次根式aa有意义的条件是a≥0若代数式有意义，则实数x的取值范围是.3x9:2a=︱a︳=(a＞0)(a=0)(a＜0)=a=0=-a10：任何实数都有立方根，a的立方根记作3a3a任何实数的立方根均只有一个11：实数的相关运算加，减，乘，除，乘方（1）a0=1(a≠0)a-p=(a≠0)1pa（2）经化简后被开方数相同的二次根式，叫同类二次根式（3）二次根式的加减就是合并同类二次根式×ab=ababab=(b≠0)12:二次根式的乘法和除法运算13:2aa=a(a＞0)(a=0)(a＜0)=0=-a312748245.2232)322()21(02cos2201232351.下列各数：①3.141、②0.33333……、③、④π、⑤、⑥、⑦0.3030003000003……(相邻两个3之间0的个数逐次增加2)中，其中是有理数的有；是无理数的有。(填序号)7525322.化简：；。34.123.在下列各式中，正确的是()A.B.C.D.2)2(24.0064.032)2(330)2()2(3321.下列语句中正确的是（）(A)－９的平方根是－３(B)９的平方根是3(C)9的算术平方根是±3(D)9的算术平方根是32、下列运算中，错误的有（）①,②，③,④(A)1个(B)2个(C)3个(D)4个1251144251442)(2222220951412511613.下列说法中正确的是（）A．是一个无理数B．函数y=的自变量x的取值范围是x≥1C．8的立方根是±2D．若点P(2，a)和点Q(b，－3)关于x轴对称，则a+b的值为5411x4.-8的立方根为（）A．2B．±2C．4D．±45.x-7的负的平方根为-2，x的值为___________6.若，则x3+2的平方根为_____330xx3．下列各式中，无意义的是（）A．B．C．D．2333)3(2)3(3104．如果＋有意义，那么代数式|x－1|＋的值为（）A．±8B．8C．与x的值无关D．无法确定1xx92)9(x5．若与|b＋2|是互为相反数，则（a－b）2＝______22a6．的相反数是______，－的倒数是______．36412324612)32)(32(2)525(2224145)81()64(13122482332021320222009394