2.13有理数的混合运算.13有理数的混合运算VIP免费

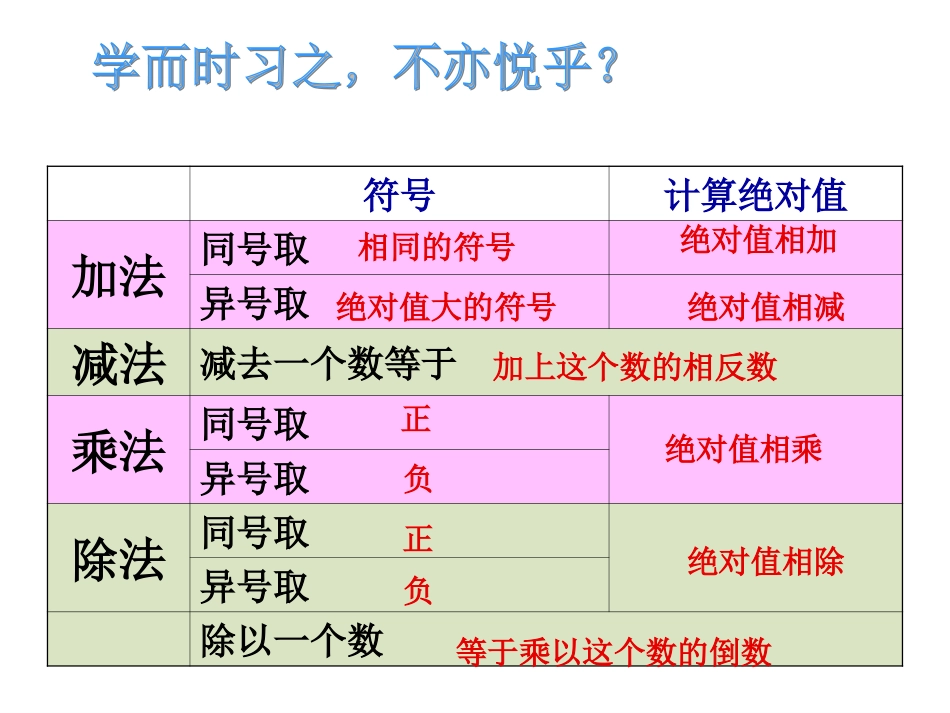
符号计算绝对值加法同号取异号取减法减去一个数等于乘法同号取异号取除法同号取异号取除以一个数相同的符号绝对值相加负绝对值相乘绝对值大的符号绝对值相减正正负绝对值相除等于乘以这个数的倒数加上这个数的相反数观察一:1512503问:1)算式中含有哪几种运算?2)运算顺序是怎样?观察二:3+5022(51)1问:1)算式含有那几种运算?2)运算顺序是怎样?乘方运算乘·除运算加·减运算3.不同级运算的运算顺序是先算___,再算___,最后算____.1.和叫做第一级运算,和____叫做第二级运算,已学过的第三级运算是____;2.同一级运算按照_____的顺序进行;从左至右4.有括号的先算_____再算_____最后算_____加减减法加法除法乘法乘方和今后会学到的开方乘方乘除小括号中括号大括号有理数混合运算的顺序指出下列各题的运算顺序(口答)236236342817110125032234501111）2）3）4）5）6）1502534281711012503223450111（1）（2）（3）4103412（4）43845101459110141509110141509110145091101250322＝－－＝－－＝－－（先算乘方）（化除为乘）（确定积的符号）（最后做加减法）（再做乘法）解原式下面是一次家庭作业的情况,请你指出他的不妥之处:1)1521252)31254312543)2982127334)62636312162121521251)2)3134312543)1382127334)6661631216(同一级运算按照从左到右的顺序进行计算)（先算括号里的)（负数的奇次方得负)（先算括号里的)5)2210526)189327)5452522216942432８）（先算乘方）2233－254552252216121241124324772222176312２）1534322１）３）431138４）45-604/32．叙述有理数的运算顺序.3．计算：―2.5×(―4.8)×(0.09)÷(―0.27)；1.复习有理数的运算律:加法的交换律:加法的结合律:乘法的交换律:乘法的结合律:乘法的分配律:a+b=b+aa+(b+c)=(a+b)+cab=ba(ab)c=a(bc)a(b+c)=ab+ac1)51(503)1()2(2分析:先算乘方,再算乘除,最后算加减.(1)(2)除以一个数等于乘以这个数的倒数;(3)在乘,除混合运算中先确定积的符号.422)(解:原式2112531)51(415031514503101411)2131)(2(分析:有括号的先算括号里的,同级运算,按照从左到右的顺序进行.解:原式341054)61(注意:在有理数乘除混合运算中,带分数一般化为假分数.3.计算)()()(388712787431怎样才可以做得又快又准：试试看试试看（3）)()()(388712787431解法一：原式3383138782473887241424212442)()()()(通分化除为乘解法二：原式338321238781277887784738781278747)()(化除为乘乘法分配律（3）)()()(388712787431哪种方法简单呢？哪种方法简单呢？1.计算：.4286348617686)2(;273199)1(三、分层练习，形成能力认真的做噢！认真的做噢！计算：.4286348617686)2(;273199)1(解：（１）原式26821827002732271002732100)(解:（２）原式860086100864234176)(本节课里我的收获是……在有理数混合运算中，先算乘方，再算乘除，乘除运算在一起时，统一化成乘法往往可以约分而使运算简化；遇到带分数通分时，可以写成整数与真分数和的形式，如―832819