勾股定理课件VIP免费

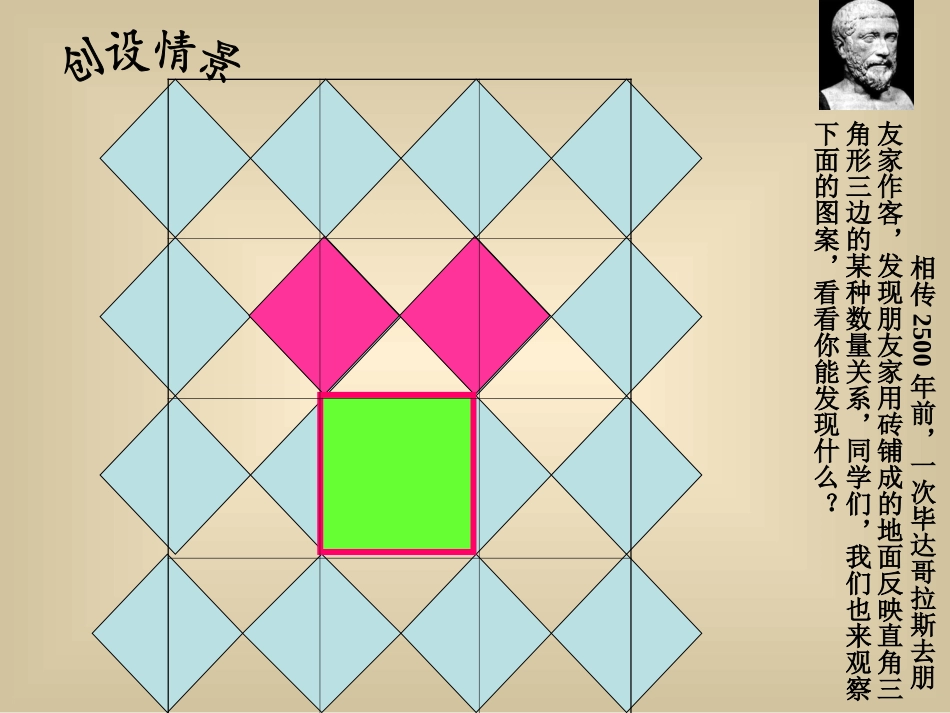
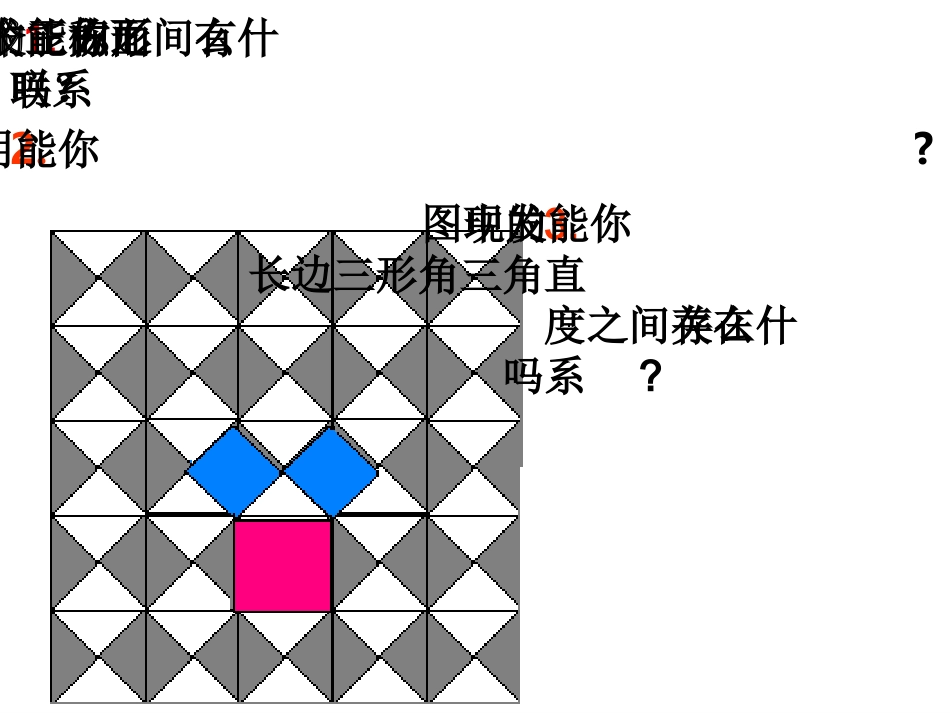
这就是本届大会会徽的图案．图1.1沁县实验中学闫红霞相传2500年前，一次毕达哥拉斯去朋友家作客，发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系，同学们，我们也来观察下面的图案，看看你能发现什么？1.你能发现图中的三个正方形的面积之间有什么联系吗？2.你能用直角三角形的边长表示正方形的面积吗?3.你能发现图中的直角三角形三边长度之间存在什么关系吗?探索勾股定理观察图2-1，回答问题：1.正方形A中含有个小方格,即A的面积是个单位面积.2.B的面积是个单位面积.C的面积是个单位面积.999ABCABC（图中每个小方格代表一个单位面积）图2-1图2-2探索勾股定理观察图2-1，回答问题：图2-1图2-2cS正方形1433218（图中每个小方格代表一个单位面积）（单位面积）分“割”成若干个直角边为整数的三角形探索勾股定理观察图2-1，回答问题：图2-1图2-2cS正方形216218（图中每个小方格代表一个单位面积）（单位面积）把C“补”成边长为6的正方形面积的一半探索勾股定理观察图2-1，回答问题：1.正方形A中含有个小方格,即A的面积是个单位面积.2.B的面积是个单位面积.C的面积是个单位面积.图2-1图2-299189探索勾股定理观察图2-2，回答问题：1.正方形A中含有个小方格,即A的面积是个单位面积.2.B的面积是个单位面积.C的面积是个单位面积.图2-1图2-24448数学家毕达哥拉斯的发现：正方形A、B、C的面积有什么关系？ABCA的面积+B的面积=C的面积SA+SB=SC直角三角形三边有什么关系？SA+SB=SCBCabcA设：等腰直角三角形的三边长分别是a、b、ca2+b2=c2ABC图2-3ABC图2-4对于一般的直角三角形是否也有这样性质呢？2．观察右边两个图并填写下表：A的面积B的面积C的面积图2-3图2-4169254913你是怎样得到表中的结果的？与同伴交流交流．图2-3图2-4cS正方形14431225cS正方形14321213在图2-3中在图2-4中C图2-3图2-4cS正方形cS正方形在图2-3中在图2-4中253421449132321425acb观察所得到的各组数据，你有什么发现？猜想两直角边a、b与斜边c之间的关系？a2+b2=c2SA+SB=SC┏a2+b2=c2acb直角三角形两直角边的平方和等于斜边的平方.勾股弦勾股定理(毕达哥拉斯定理)练习：1、求下列图中字母所表示的正方形的面积169=625A40022522581B=1442、求出下列直角三角形中未知边的长度68x5x13解：由勾股定理得：x2=36+64x2=100x2=62+82∴x=10∵x2+52=132∴x2=132-52x2=169-25x2=144∴x=12∵x>0∵x>0（1）谈谈本节课你有什么收获？（2）你还有什么困惑？（1）课后练习1，2（2）习题14.1中2，3，4，5