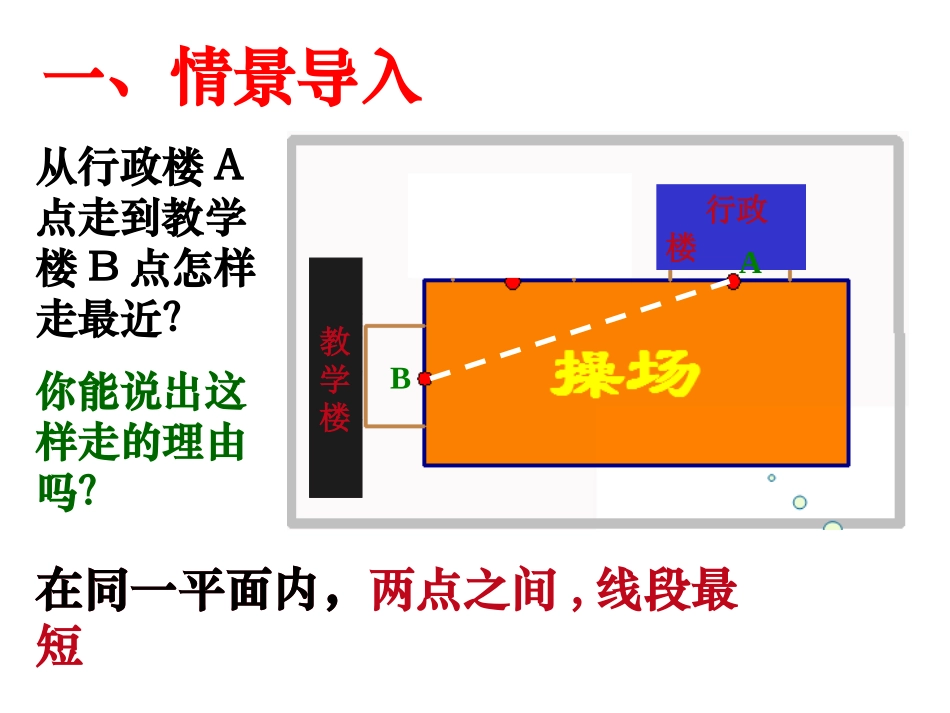
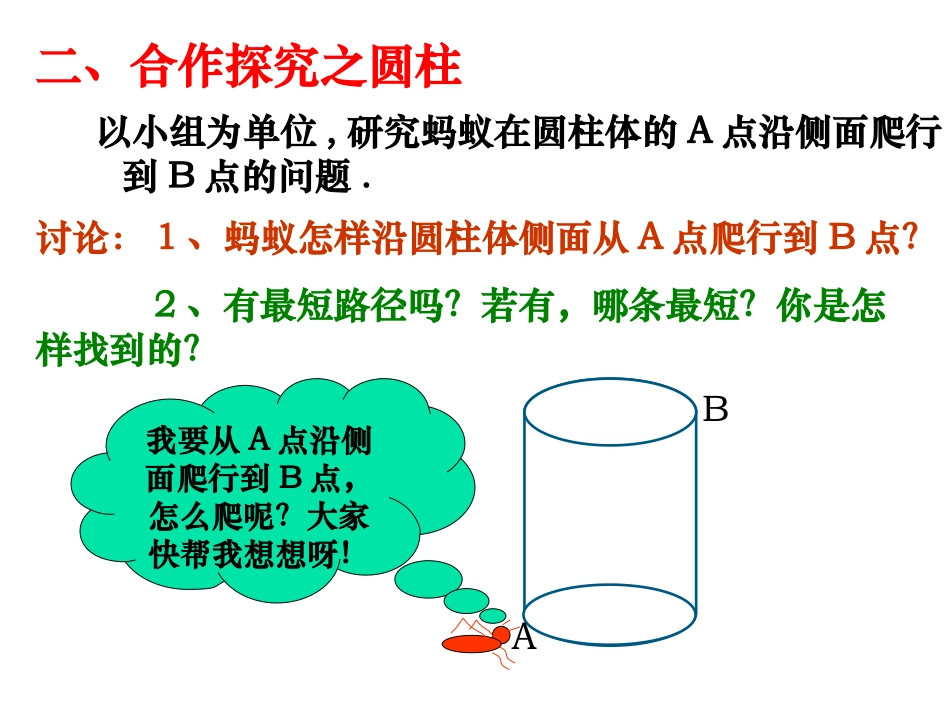
在同一平面内,两点之间,线段最短一、情景导入从行政楼A点走到教学楼B点怎样走最近?教学楼行政楼BA你能说出这样走的理由吗?在同一平面内,以小组为单位,研究蚂蚁在圆柱体的A点沿侧面爬行到B点的问题.二、合作探究之圆柱讨论:1、蚂蚁怎样沿圆柱体侧面从A点爬行到B点?2、有最短路径吗?若有,哪条最短?你是怎样找到的?BA我要从A点沿侧面爬行到B点,怎么爬呢?大家快帮我想想呀!圆柱爬行路径:(1)(2)(3)(4)ABABABAB例题(圆柱体侧面爬行路径最短问题)例1:如图所示,有一个圆柱,它的高是12cm,底面上圆的周长等于18cm,在圆柱下底面的点A处有一只蚂蚁,它想吃到上底面上与点A相对的点B处的食物,沿圆柱侧面爬行到B点,求其爬行的最短路程是多少?12h例题解析C解:由题意得展开图,知AB即为最短路径,其中AC=12,BC=91821AB=15=225=AB+9=12+BCAC中,由勾股定理可得在22222:ABCRt所以蚂蚁爬行的最短路径是15cm。转化12hBA例题变式方法总结:侧面展开图中两点之间的连线段最短。讨论:1、蚂蚁怎样沿正方体表面从A点爬行到G点?2、有最短路径吗?若有,那条最短?你是怎么确定呢?三、合作探究之正方体ABCDEFGH以小组为单位,研究蚂蚁在正方体的A点沿表面爬行到B点的问题.正方体爬行路径ABFEHGABCDEFGH前(后)上(下)ABCDEFGHDAEHGFABCDEFGH右(左)上(下)前(后)右(左)BCAEFG例题变式:ABCD124GFEH(1)、如把正方体变成如左图的长方体,长方体底面长为2,宽为1,高为4,蚂蚁从A点沿长方体表面爬到E点有多少种爬行可能?那种爬行路径的距离最短?是多少?解:长方体侧面展开图一共有三种情况,如上图,其距离分别是:第一种:第二种:第三种:例题变式:ABCD124GFEHDAGHFE241左(右)上(下)(1)BAGFHE241前(后)上(下)(2)ABCFGE412前(后)右(左)(3)总结:四棱柱给出的长、宽、高三个数据,把较小的两个数据的和作为一条直角边的长,最大的数据作为另一条直角边的长,这时斜边的长即为最短距离。有一只蚂蚁从一个正方体的顶点A沿表面爬到顶点C,如果底面是一个边长为4厘米的正方形,高为6厘米?则蚂蚁所爬的最短路径是多少厘米?AC2、注意:运用勾股定理解决实际问题时,①、没有图的要按题意画好图并标上字母;②、有时必须设好未知数,并根据勾股定理列出相应的方程式才能做出答案。六、归纳总结1、数学思想:数学问题转化实际问题