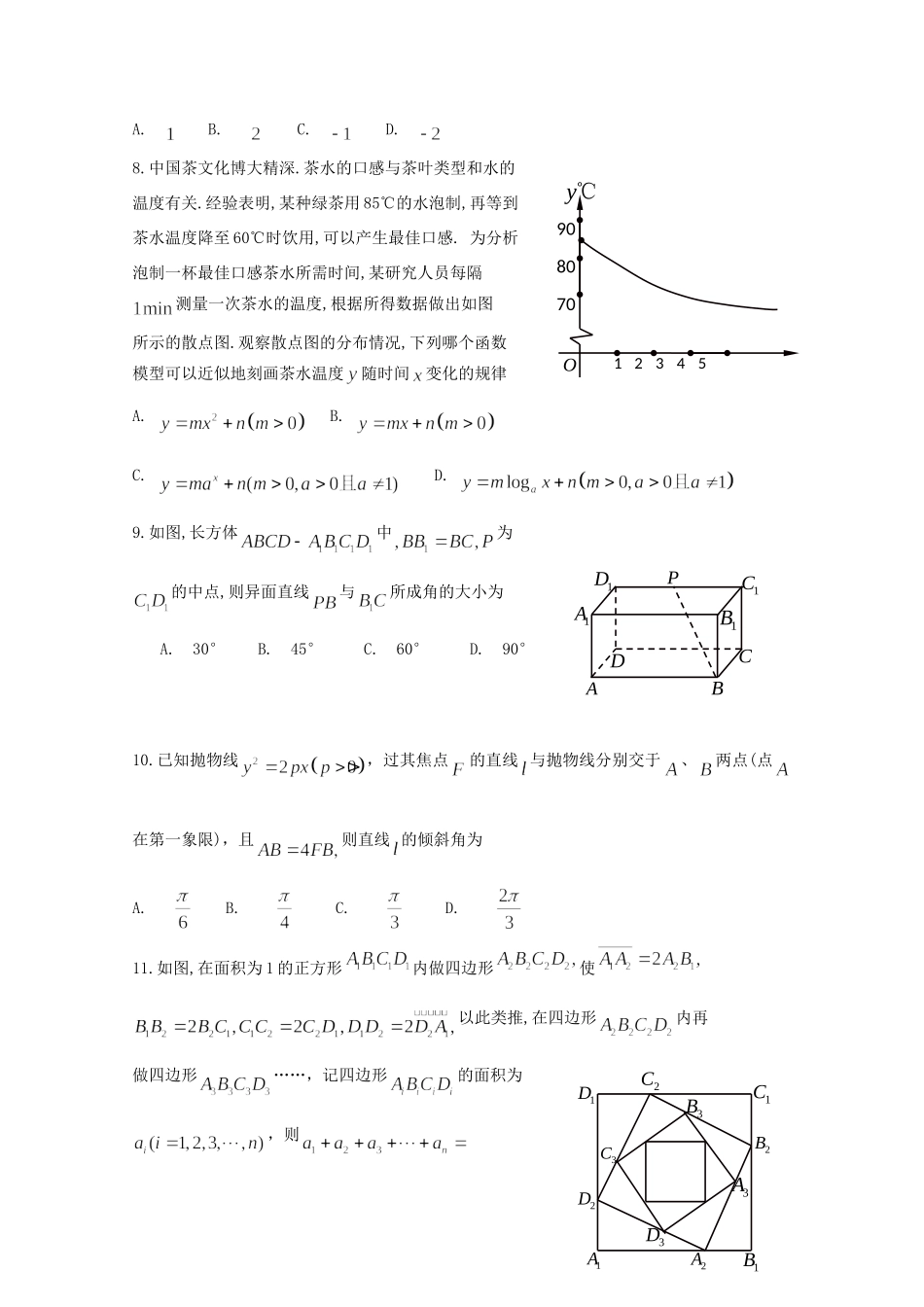
吉林省长春市2021届高三数学第一次质量监测(一模)试题文一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合则集合的元素个数有A.1个B.2个C.3个D.4个2.若平面向且,则的值为3.函数的图象的一条对称轴是A.B.C.D.4.已知双曲线的渐近线方程为则其离心率为A.B.C.D.5.张老师居住的一条街上,行驶着甲、乙两路公交车,这两路公交车的数目相同,并且都是每隔十分钟就到达车站一辆(即停即走).张老师每天早晨都是在6:00到6:10之间到达车站乘车到学校,这两条公交线路对他是一样的,都可以到达学校,甲路公交车的到站时间是6:09,6:19,6:29,6:39,…,乙路公交车的到站时间是6:00,6:10,6:20,6:30,…,则张老师乘坐上甲路公交车的概率是A.10%B.50%C.60%D.90%6.将长、宽分别为和的长方形沿对角线折起,得到四面体,则四面体的外接球体积为A.B.C.D.7.曲线在处的切线的斜率为A.B.C.D.8.中国茶文化博大精深.茶水的口感与茶叶类型和水的温度有关.经验表明,某种绿茶用85℃的水泡制,再等到茶水温度降至60℃时饮用,可以产生最佳口感.为分析泡制一杯最佳口感茶水所需时间,某研究人员每隔测量一次茶水的温度,根据所得数据做出如图所示的散点图.观察散点图的分布情况,下列哪个函数模型可以近似地刻画茶水温度随时间变化的规律A.B.C.D.9.如图,长方体中为的中点,则异面直线与所成角的大小为A.30°B.45°C.60°D.90°10.已知抛物线,过其焦点的直线与抛物线分别交于、两点(点在第一象限),且则直线的倾斜角为A.B.C.D.11.如图,在面积为1的正方形内做四边形使以此类推,在四边形内再做四边形……,记四边形的面积为,则1C1D1A1B2A2B2C2D3A3B3C3D90807012345Oy℃ABCD1A1B1C1DP12.已知定义在上的函数满足当时当时则二、填空题:本题共4小题,每小题5分,共20分.13.若则.14..15.若复数满足则.16.已知是数列的前项和,满足,则;数列的前项和.三、解答题:共70分,解答应写出文字说明、证明过程或演算步骤.第17-21题为必考题,每个试题考生都必须作答.第22-23题为选考题,考生根据要求作答.(一)必考题:共60分17.(12分)如图,在四棱锥中,底面为正方形,⊥底面,,为的中点,为线段上的动点.(I)求证:平面平面;(Ⅱ)求点到平面的距离.18.(12分)在中,角的对边分别为,且满足.(1)求角;(Ⅱ)若,求外接圆的半径.19.(12分)某小区超市采取有力措施保障居民正常生活的物资供应.为做好日常生活必需的甲类物资的供应,超市对社区居民户每天对甲类物资的购买量进行了调查,得到了以下频率分布直方图(如图).(I)估计该小区居民对甲类物资购买量的中位数;(Ⅱ)现将小区居民按照购买量分为两组,即购买量在单位:)的居民为A组,购买量在(单位:]的居民为B组,采用分层抽样的方式从该小区中选出5户进行生活情况调查,再从这5户中随机选出3户,求选出的B组户数为2的概率.PABCDEF123456购买量/kg0.300.250.200.150.10频率/组距20.(12分)已知椭圆,直线分别与轴轴交于两点,与椭圆交于两点.(I)若求直线的方程;(Ⅱ)若点的坐标为求面积的最大值.21.(12分)设函数.(I)当时,求函数的单调区间;(Ⅱ)当时,求证:(二)选考题:共10分,请考生在22、23题中任选一题作答,如果多做则按所做的第一题计分.22.【选修4-4坐标系与参数方程](10分)已知直线的参数方程为(为参数),以坐标原点为极点,轴的非负半轴为极轴建立极坐标系,圆的极坐标方程为(I)求直线的普通方程和圆的直角坐标方程;(Ⅱ)若直线与圆相交于两点,求23.[选修4-5不等式选讲](10分)已知(I)求证:;(Ⅱ)求证:.长春市2021届高三质量监测数学(文科)试题参考答案及评分参考一,选择题(本大题共12小题,每小题5分,共60分)1.A.【解题思路】所以故选A.2.C【解题思路】由可知即,故选C.3.C【解想思路】令则,故选C.4.B【解题思路】由渐近线方程可知故选B.5.D【解思路】张老师到达车站在6:00-6:10中是等可能的,故张老师在6:00-6:09到达车站的概率为90%,故有90%的可能乘坐甲路公交车,故选D6.A【解题思路】中点到A,B,C,D的距离均为1,故球的体积为,故选A.7.B【解题思路】当x=e时,k=2,故选B.8.C由函数图象可知符合条件只有指数函数,故选C9.D【解题思路】⊥平面平面即故选D10.C【解题思路】如图,...