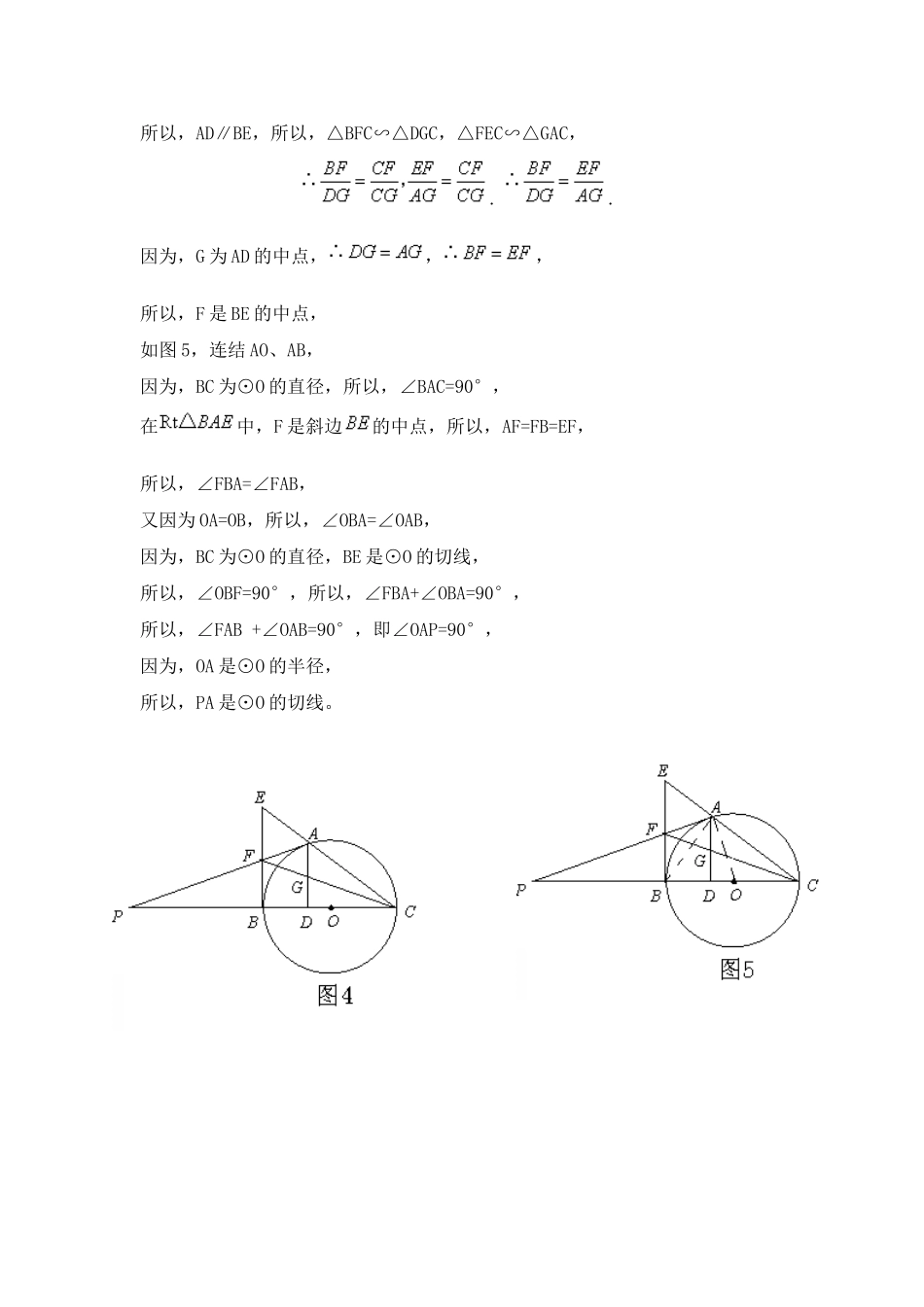
走进垂直证切线直线和圆有三种位置关系:相交、相切和相离。特别是判断一条直线是圆的切线,是近几年中考的常见题型。下面我们就一起走进圆的切线,仔细寻找判断的方法。切线的判定定理:经过半径的外端,并且和这条半径垂直的直线,是圆的切线.是判断一条直线是否是圆的切线最常用的依据。所以,在运用判定时,要紧紧抓住两个要素:①被判断直线必须经过圆上的某一个点;②被判断直线必须与直线所过圆上的点所在的圆的半径或直径垂直。如何深挖题目的条件,综合优选所学知识,证明直线与所在的圆的半径或直径垂直,是问题解决的核心。请同学们在阅读下面的问题时,仔细体会是如何突破关键,证垂直的。例1、如图1,AB为⊙O的直径,弦CD⊥AB于点M,过点B作BE∥CD,交AC的延长线于点E,连结BC。求证:BE为⊙O的切线。(07山东济宁改编)分析:被判断的直线是BE,由于AB为⊙O的直径,所以,直线BE已经具备了第一个条件:经过圆上的某一个点。这样,问题的关键就是证明第二个条件:AB⊥BE。证明:因为AB为⊙O的直径,所以,点B是圆上的一个点,所以,直线BE经过了圆上的点B;因为,弦CD⊥AB于点M,所以,∠CMB=90°,因为,BE∥CD,所以,∠CMB+∠EBA=180°,所以,∠EBA=90°,因为AB为⊙O的直径,所以,BE为⊙O的切线。例2、如图2,已知:△ABC内接于⊙O,点D在OC延长线上,sinB=21,∠D=30°。求证:AD是⊙O的切线。(07福建福州改编)分析:被判断的直线是AD,由于△ABC内接于⊙O,所以,直线AD已经具备了第一个条件:经过圆上的某一个点。这样,问题的关键就是证明第二个条件:AD⊥OA。证明:如图3,连结OA,在△ABC中,因为∠B是锐角,且,sinB=21,所以,∠B=30°,因为,∠B和∠AOC是弧AC所对的圆周角和圆心角,所以,∠AOC=2∠B,因为,∠B=30°,所以,∠AOC=60°,在△AOD中,∠AOD+∠D+∠OAD=180°,所以,∠OAD=180°-(∠AOD+∠D)=180°-60°-30°=90°,所以,AD⊥OA,所以,AD是⊙O的切线。例3、如图4,A是以BC为直径的⊙O上一点,AD⊥BC于点D,过点B作⊙O的切线,与CA延长线相交于点E,G为AD的中点,连结CG延长与BE交于点F,延长AF和CB延长线相交于点P。求证:PA是⊙O的切线。(07四川成都)分析:被判断的直线是PA,由于A是以BC为直径的⊙O上一点,所以,直线PA已经具备了第一个条件:经过圆上的某一个点。这样,问题的关键就是证明第二个条件:PA⊥OA。证明:因为,BC为⊙O的直径,BE是⊙O的切线,所以,EB⊥BC,又因为,AD⊥BC,所以,AD∥BE,所以,△BFC∽△DGC,△FEC∽△GAC,..因为,G为AD的中点,,,所以,F是BE的中点,如图5,连结AO、AB,因为,BC为⊙O的直径,所以,∠BAC=90°,在中,F是斜边的中点,所以,AF=FB=EF,所以,∠FBA=∠FAB,又因为OA=OB,所以,∠OBA=∠OAB,因为,BC为⊙O的直径,BE是⊙O的切线,所以,∠OBF=90°,所以,∠FBA+∠OBA=90°,所以,∠FAB+∠OAB=90°,即∠OAP=90°,因为,OA是⊙O的半径,所以,PA是⊙O的切线。