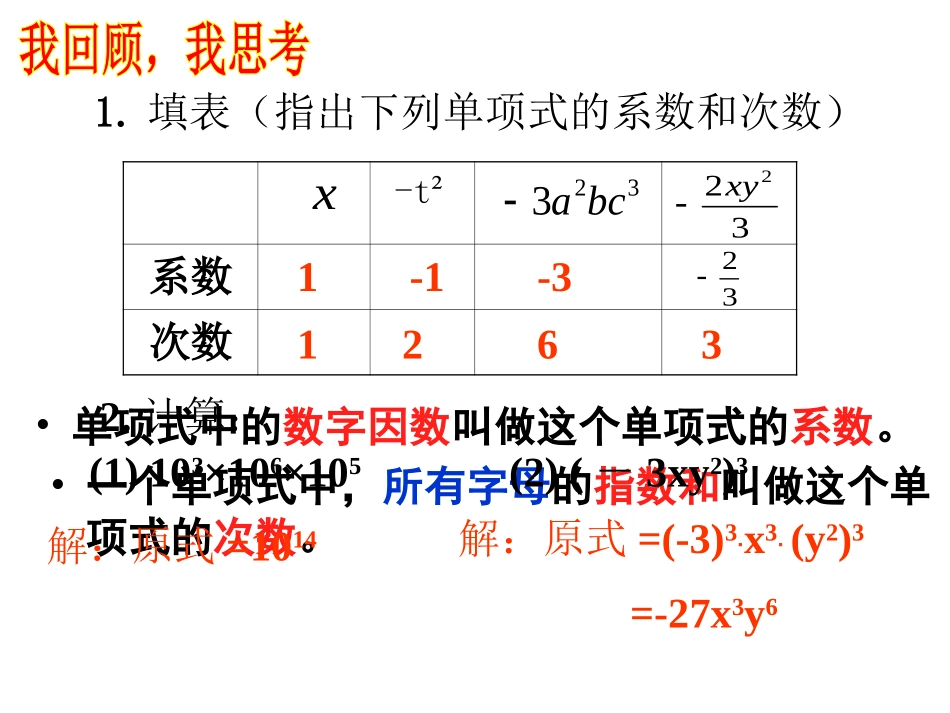
每学到一个数学难点的时候,尝试着对别人讲解这个知识点并让他理解——你能讲清楚才说明你真的理解了。不要因为题目“很小”就不遵循某些你不熟练的解题规范——好习惯是培养出来的,而不是一次记住的。1.填表(指出下列单项式的系数和次数)•单项式中的数字因数叫做这个单项式的系数。•一个单项式中,所有字母的指数和叫做这个单项式的次数。-t²系数次数x323bca322xy11-12-363232.计算:(1)103×106×105(2)(-3xy2)3解:原式=1014解:原式=(-3)3·x3·(y2)3=-27x3y63.光的速度约为3×105千米/秒,太阳光照射到地球上需要的时间大约是5×102秒,你知道地球与太阳的距离约是多少千米吗?解:(3×105)×(5×102)=3×5×105×102=(3×5)×(105×102)=15×107=1.5×108(乘法交换律)(乘法结合律)(同底数幂的运算性质)即地球与太阳的距离约是1.5×108千米.模仿刚才的做法,尝试计算:(1)2a2·3a3(2)4x2·(-3xy3)(3)(-5ab3)·(-4b2c)通过计算,尝试总结单项式乘以单项式的法则.1.课本99页练习第2题2.计算:(1)(-5x2y)(-3x)(2)(2a)3(-5ab2)(3)(-2x)3(-5xy2)3.课本99页练习第1题奖励2:(-2x2y)3(2xyz)(-2x2y)奖励1:(3×105)×(5×102)奖励1:(3×105)×(5×102)解:原式=-8x6y3·2xyz·(-2x2y)=[-8×2×(-2)](x6·x·x2)(y3·y·y)·z原式=(3×5)(105×102)=15×107=32x9y5z=1.5×108奖励2:(-2x2y)3(2xyz)(-2x2y)(-a)2·a3·(-2b)3-(-2ab)2·(-a)3b解:原式=a2a3·(-8b3)-4a2b2·(-a3b)=-8a5b3+4a5b3=-4a5b32.计算:1.已知3xn-3y5-n与-8x3my2n的积是2x4y9的同类项,求m、n的值.计算:(-a)2·(a3-2b3)必做题:1、阅读教材98—99页内容,圈画重点部分。2、习题14.1第3题。选做题:已知求m、n的值。,)2()(41942132yxxyyxnm本节课我们学习了哪些内容?1、如何进行单项式与单项式的乘法运算?2、单项式与单项式相乘的过程中,应用了哪些运算律和运算性质?3、在这部分学习中,我们应该注意哪些问题?