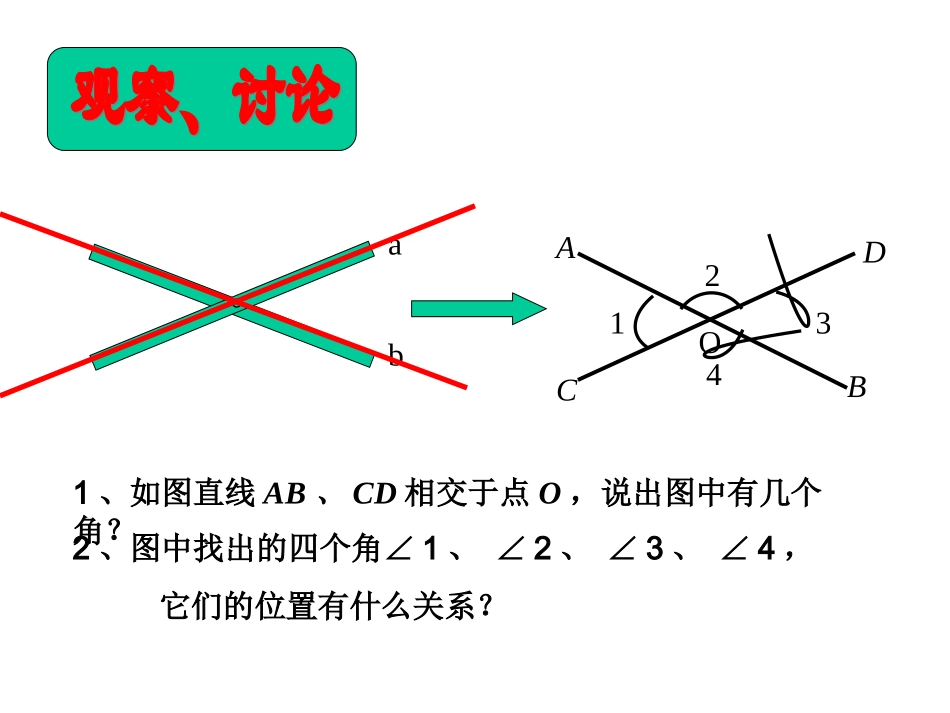
5.1.1相交线1、理解对顶角与邻补角概念2、会利用说理解释对顶角相等3、利用对顶角、邻补角的性质解决实际问题。ab1、如图直线AB、CD相交于点O,说出图中有几个角?12342、图中找出的四个角∠1、∠2、∠3、∠4,它们的位置有什么关系?ABCDO∠1和∠3∠2和∠4有一个公共顶点,一个角的两边分别是另一个角的两边的反向延长线∠1和∠2∠2和∠3∠3和∠4∠4和∠1有一个公共顶点,还有一条公共边,它们的另一条边互为反向延长线23ABCD14互为对顶角互为邻补角3、图中∠AOC和∠BOC是什么关系的角?OBC·A12344、图中∠1的邻补角有几个?哪几个?是什么关系的角?你有什么结论?5、右图中∠1和∠3、∠2和∠4是对顶角,观察此图,你能猜想出∠1和∠3、∠2和∠4的大小关系吗?对顶角相等对顶角相等这个推理过程可以写成:∵∠1与∠2互补,∠3与∠2互补对顶角的性质:(邻补角定义)(同角的补角相等)∴∠1=3∠ba1423例:如图,直线a、b相交,∠1=40°,求∠2、∠3、∠4的度数。解:∵直线a、b相交∴∠1+2=180∠°∵∠1=40°∴∠2=180°-1∠=180°-40°=140°∵∠2与∠4是对顶角∴∠4=2=140∠°∵∠3与∠1是对顶角∴∠3=1=40∠°如图,取两根木条a、b,将它们钉在一起,并把他们想象成两条直线,就得到一个相交线的模型,你能说出其中的一些邻补角与对顶角吗?如果其中一个角是35°,其它三个角各是多少度?这个角是90º、115°、m°呢?。ab角的名称特征性质相同点不同点对顶角邻补角①两条直相交而成的角②有一个公共顶点③没有公共边①两条直相交而成的角②有一个公共顶点③有一条公共边对顶角相等邻补角互补都是两条直线相交而成的角,都有一个公共顶点,他们都成对出现对顶角没有公共边而邻补角有一条公共边两条直线相交时,一个角的对顶有一个,而一个角的邻补角有两个必做作业:教材第7页习题5.1第1、2题;选做作业:作业卷