1522完全平方公式VIP免费

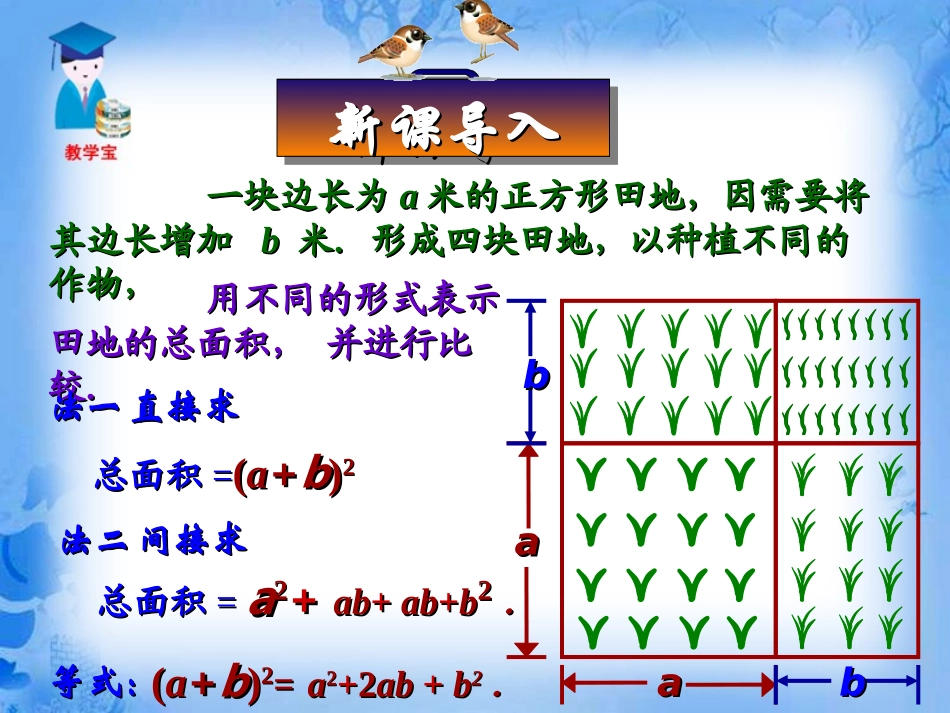
新课导入新课导入新课导入新课导入一块边长为一块边长为aa米的正方形田地，因需要将米的正方形田地，因需要将其边长增加其边长增加bb米．形成四块田地，以种植不同的米．形成四块田地，以种植不同的作物，作物，aaaabbbb用不同的形式表示用不同的形式表示田地的总面积，并进行比田地的总面积，并进行比较．较．法一法一直接求直接求总面积总面积==((aa++bb))22法二法二间接求间接求总面积总面积==aa22++abab++abab++bb22．．((aa++bb))22==aa22++22abab++bb22．．等式：等式：添括号法则：利用添括号法则灵活应用完全平方公式．知识与能力知识与能力教学目标教学目标教学目标教学目标利用去括号法则得到添括号法则，培养逆向思维能力，进一步熟悉乘法公式，体会公式中字母的含义．过程与方法过程与方法1．在计算过程中发现规律，并能用符号表示，从而体会数学的简捷美．2．算法多样化，培养多方位思考问题的习惯，提高合作交流意识和创新精神．情感态度与价值观情感态度与价值观理解添括号法则，进一步熟悉乘法公式的合理利用．重点重点难点难点教学重难点教学重难点教学重难点教学重难点1．在多项式与多项式的乘法中适当添括号达到应用公式的目的．2．理解完全平方公式的结构特征，灵活应用完全平方公式．一般地，我们有一般地，我们有（（aa＋＋bb））22=a=a22＋＋2ab2ab＋＋bb22（（aa－－bb））22=a=a22－－2ab2ab＋＋bb22即两数和（或差）的平方，等于它即两数和（或差）的平方，等于它们的平方和，加（或减）它们的积的们的平方和，加（或减）它们的积的22倍．倍．这两个公式叫做（乘法的）完全这两个公式叫做（乘法的）完全平方公式．平方公式．知识要知识要点点知识要知识要点点aaaabbbbaa22ababababbb22(a+b)2=aa−−bbaa−−bbaaaaaabbbb((aa−−bb))bbbb((aa−−bb))22a2+2ab+b2即(a−b)2=a2−2ab+b2(a−b)2=a2−ab−b(a−b)例1运用完全平方公式计算（1）（2a＋b）2（2）（y－2）2解：（1）（2a＋b）2（2）（y－2）2=(2a)2＋2×2ab＋b2=4a2＋4ab＋b2=y2－2y2＋4=y2－4y＋4例2计算（1）3052=(300+5)2=3002+2×300×5+52=90000+1500+25=91525（2）1012=(100+1)2=1002+2×100×1+12=10000+200+1=10201（3）2032=(200+3)2=2002+2×200×3+32=40000+1200+9=41209（4）10072=(1000+7)2=10002+2×1000×7+72=1000000+14000+49=1014049A．4B．-4C．0D．4或-4AA（1）已知(a+b)2=21，(a-b)2=5，则ab=()练一练一练练练一练一练练（2）如果a+a1=4，则a2+a21=()A．14B．9C．10D．11AA（3）若2a2-2ab+b2-2a+1=0则a、b分别为（）A．1，-1B．1，1C．-1，1D．0，0BB（4）已知x=a+2b，y=a-2b，求：x2+xy+y2．解：x2+xy+y2=(a+2b)2＋（a＋2b）（a-2b）＋(a-2b)2=(a2＋4ab＋4b2)+(a2－4b2)+(a2－4ab＋4b2)=3a2＋4b2c2a2abacabb2bcbcacabcabc三数和的平方公式：(a+b+c)2=a2+b2+c2+2ab+2bc+2ca立方和（差）公式立方和（差）公式二次三项型乘法公式二次三项型乘法公式(x+a)(x+b)=x2+(a+b)x+ab（a±b）(a2ab+b2)=a3±b311．完全平方公式．完全平方公式(a±b)2=a2±2ab+b2两项和或差的平方等于这两项的平方和加上或减去它们的积的2倍．22．三项完全平方公式．三项完全平方公式(a+b+c)2=a2+b2+c2+2ab+2ac+2bc课堂小结课堂小结课堂小结课堂小结2．如果25a²-30ab+m是一个完全平方式，则m=______.3．16x²+_______+25y²=_________²1．如果x²+ax+16是一个完全平方式，则a=___.±±889m9m22±±40xy40xy(4x(4x±±5y)5y)随堂练习随堂练习随堂练习随堂练习4．已知：a+b=8，ab=15，则a2+b2的值为_____，(a-b)2的值为________.4949445．已知：a=2005x+2004，b=2005x+2005，c=2005x+2006，那么a2+b2+c2-ab-ac-bc的值（）．A．1B．2C．3D．4CC6．已知x2+y2-2x+2y+2=0，则x2002+y2003的值为（）A．0B．1C．2D．4AA7．9972=(1000-3)2=10002-2×1000×3+32=1000000-6000+9=9940098．1942=(200-6)2=2002-2×200×6+62=40000-2400+36=376369．9932=(1000-7)2=10002-2×1000×7+72=1000000-14000+49=98604910．982=(100-2)2=1002-2×100×2+22=10000-400+4=960411．(a+b)(a-c)=a2+ab-ac-bc13．(xy-z)(xy+z)=x...