第十五章--整式.1.1单项式VIP免费

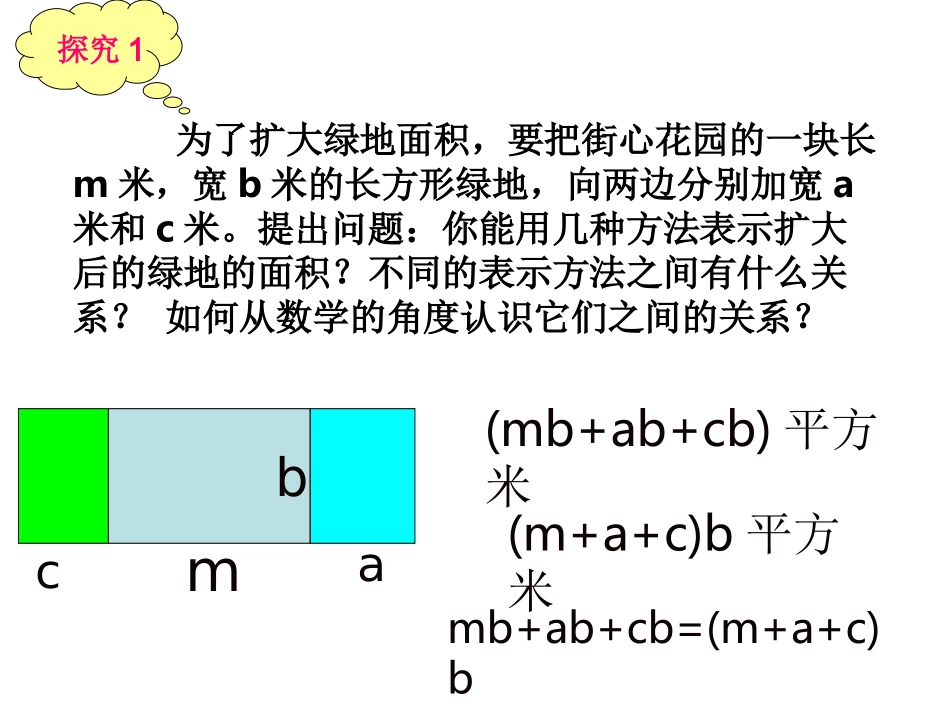
第十五章整式为了扩大绿地面积，要把街心花园的一块长m米，宽b米的长方形绿地，向两边分别加宽a米和c米。提出问题：你能用几种方法表示扩大后的绿地的面积？不同的表示方法之间有什么关系？如何从数学的角度认识它们之间的关系？mbac(mb+ab+cb)平方米(m+a+c)b平方米mb+ab+cb=(m+a+c)b探究11.若正方形的边长为x，那么正方形的周长为。2.一辆汽车的速度是v千米/小时，行使t小时所走过的路程是千米。3.若n表示一个数，则它的相反数是。4.若正方形的棱长为a，它的表面积为，体积为。5.直径为m的圆面积是()。4xvt-n6a2a34πm2思考14xvt-n6a2a34πm2t-53x+5y+2z21ab–πr2如果把上面的式子分类，你认为能分几类？你的分类标准是什么？探究24xvt-n6a2a34πm2上面的式子都是数与字母的积，这样的式子叫做单项式。单独的一个数或一个字母也是单项式。定义1我们把单项式中的数字因数叫做这个单项式的系数。上面每个单项式的系数分别是多少？（1）圆周率是常数。（2）如果单项式是单独的字母，那么它的系数是1。如：单项式c的系数是1。（3）当一个单项式的系数是1或–1时，“1”通常省略不写，但不要误认为是0，如a²，–abc；（4）单项式的系数是带分数时，应写成假分数。注意1•一个单项式中，所有字母的指数的和叫做这个单项式的次数。4xvt-n6a2a34πm2猜一猜：这六个单项式的次数分别是多少？探究3رىبىنىسىدنىغىيڭىنىرىلچۈكتەسرۆكەجىرەدڭىنرەلپرەھقىلرابىكىتقىلازەئرىب.زىمياتائپەدىسىجىرەدڭىنقىلازەئ判断下列各式是否是单项式。如果不是，请简要说明理由；如果是，请指出它的系数与次数：abcyx（2）a4r2（3）(1)(4)(5)(6)3223yzx73a2b3（7）53（8）a练习1给你一个数5和字母n你能组成几个单项式呢？探究4它们的系数和次数分别是多少？33a22x22n0xba21你能对下列单项式进行分类吗？考考你:1、判断下列说法是否正确：（1）单项式a既没有系数，也没有次数。（2）单项式5X105x的系数是5。（3）-2005是单项式。（4）单项式的系数是，次数是32、写一个单项式，使它的系数为-4，次数为5。232x32；ab33)1(2的系数是；xy0)2(2的系数是；r2121)3(2的系数是；cab次的次数是23)4(2；次的次数是单项式33)5(3练习：判断正误，错误的改正。