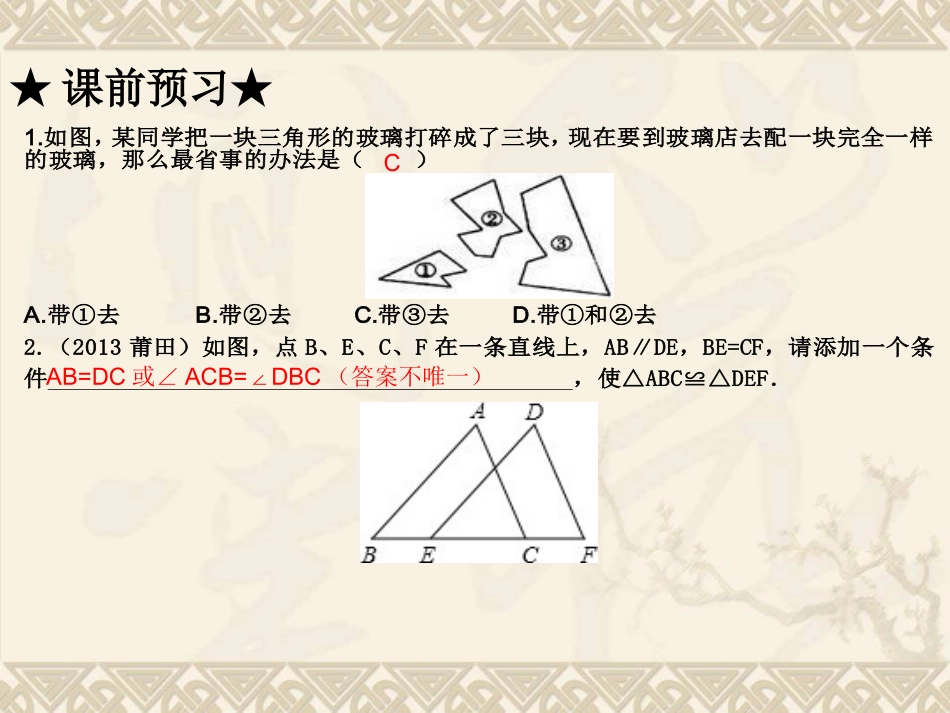
第二部分空间与代数第四章三角形第15讲全等三角形高分突破在手中考高分无忧⊙考纲要求⊙了解全等三角形的概念,探索并掌握两个三角形全等的条件.⊙命题趋势⊙2010~2013年广东省中考题型及分值统计1.从近几年的广东省考试内容来看,本讲内容命题难度适中,考查的重点是找全等三角形和全等三角形的性质与证明.2.题型以解答题为主.3.2014年考查重点可能是对全等三角形概念的理解,找全等三角形;掌握两个三角形全等的条件,证明两个三角形全等,全等三角形性质的应用.★中考导航★年份试题类型知识点分值2010解答题全等三角形的判定与性质7分2011解答题全等三角形的判定6分2012解答题全等三角形的判定9分2013解答题全等三角形的判定5分★课前预习★1.如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是()A.带①去B.带②去C.带③去D.带①和②去2.(2013莆田)如图,点B、E、C、F在一条直线上,AB∥DE,BE=CF,请添加一个条件,使△ABC≌△DEF.CAB=DC或∠ACB=DBC∠(答案不唯一)3.(2013玉林)如图,AB=AE,∠1=∠2,∠C=∠D.求证:△ABC≌△AED.3.证明: ∠1=∠2,∴∠1+∠EAC=∠2+∠EAC,即∠BAC=∠EAD, 在△ABC和△AED中,AEABEADBACCD∴△ABC≌△AED(AAS).4.(2013珠海)如图,已知,EC=AC,∠BCE=∠DCA,∠A=∠E;求证:BC=DC.4.证明: ∠BCE=∠DCA,∴∠BCE+∠ACE=∠DCA+∠ACE,即∠ACB=∠ECD,在△ABC和△EDC中,EAACECECDACB∴△ABC≌△EDC(ASA),∴BC=DC.★考点梳理★1.全等三角形的定义:能完全重合的两个三角形叫做全等三角形.2.全等三角形的判定方法(1)有两边和它们的夹角对应相等的两个三角形全等(简称“”)(2)有两角和它们的夹边对应相等的两个三角形全等(简称“”)(3)有两角和其中一角的对边对应相等的两个三角形全等(简称“”)(4)有三边对应相等的两个三角形全等(简称“”)(5)有斜边和一条直角边对应相等的两个直角三角形全等(简称“”)3.全等三角形的性质(1)全等三角形的对应边、对应角相等;(2)全等三角形的对应角平分线、对应中线、对应高线相等;(3)全等三角形的周长相等、面积相等.SASASAAASSSSHL考点1.全等三角形的判定(2007、2009~2013年考)1.(2013绥化)如图,A,B,C三点在同一条直线上,∠A=∠C=90°,AB=CD,请添加一个适当的条件,使得△EAB≌△BCD.思路点拨:本题主要考查了全等三角形的判定,开放型题目,根据不同的三角形全等的判定方法可以选择添加的条件也不相同.★课堂精讲★AE=CB(答案不唯一)2.(2013佛山)课本指出:公认的真命题称为公理,除了公理外,其他的真命题(如推论、定理等)的正确性都需要通过推理的方法证实.(1)叙述三角形全等的判定方法中的推论AAS;(2)证明推论AAS.要求:叙述推论用文字表达;用图形中的符号表达已知、求证,并证明,证明对各步骤要注明依据.思路点拨:(1)两边及其夹角分别对应相等的两个三角形全等.(2)根据三角形内角和定理和全等三角形的判断定理ASA来证明.2.解:(1)三角形全等的判定方法中的推论AAS指的是:两角及其中一角的对边对应相等的两个三角形全等.(2)已知:在△ABC与△DEF中,∠A=∠D,∠C=∠F,BC=EF.求证:△ABC≌△DEF.证明:如图,在△ABC与△DEF中,∠A=∠D,∠C=∠F(已知),∴∠A+∠C=∠D+∠F(等量代换).又 ∠A+∠B+∠C=180°,∠D+∠E+∠F=180°(三角形内角和定理),∴∠B=∠E. 在△ABC与△DEF中,EBEFBCFC∴△ABC≌△DEF(ASA).考点2.全等三角形的性质(2009~2012年考)3.(2013深圳)如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的三个项点分别在这三条平行直线上,则sinα的值是()A.31B.176C.55D.1010思路点拨:过点A作AD⊥l1于D,过点B作BE⊥l1于E,根据同角的余角相等求出∠CAD=∠BCE,然后利用“角角边”证明△ACD和△CBE全等,根据全等三角形对应边相等可得CD=BE,然后利用勾股定理列式求出AC,再根据等腰直角三角形斜边等于直角边的2倍求出AB,...