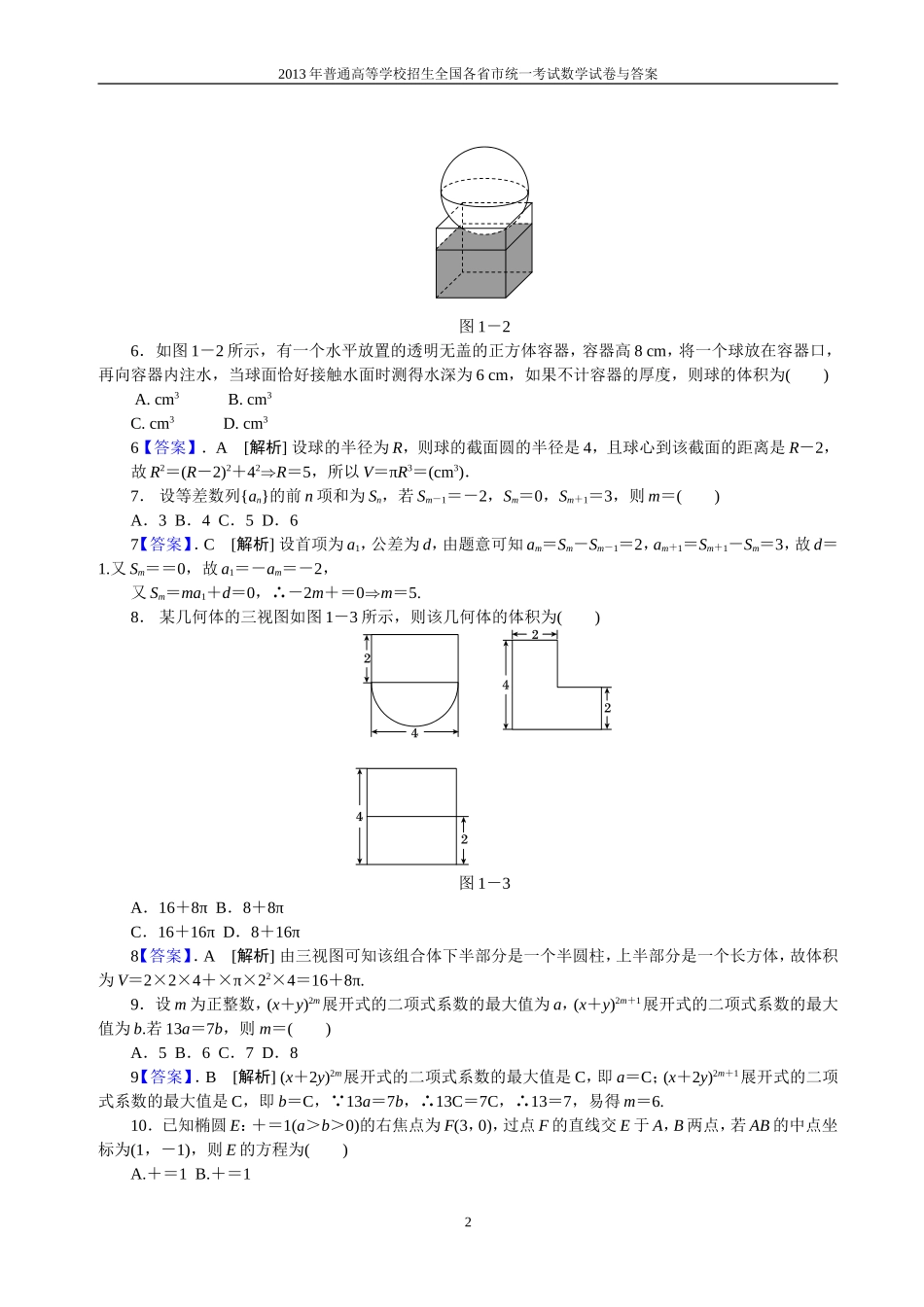
2013年普通高等学校招生全国各省市统一考试数学试卷与答案2013年普通高等学校招生全国统一考试(新课标Ⅰ卷)(理科数学)精校精析一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一个是符合题目要求的.1.已知集合,,则(A)∅(B)(C)(D)1【答案】.B[解析]A={x|x<0或x>2},故2.若复数z满足(3-4i)z=|4+3i|,则z的虚部为()A.-4B.-C.4D.2【答案】.D[解析]z====+i,故z的虚部是.3.为了解某地区的中小学生的视力情况,拟从该地区的中小学生中抽取部分学生进行调查,事先已了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异,而男女生视力情况差异不大.在下面的抽样方法中,最合理的抽样方法是()A.简单随机抽样B.按性别分层抽样C.按学段分层抽样D.系统抽样3【答案】.C[解析]因为总体中所要调查的因素受学段影响较大,而受性别影响不大,故按学段分层抽样.4.已知双曲线C:-=1(a>0,b>0)的离心率为,则C的渐近线方程为()A.y=±xB.y=±xC.y=±xD.y=±x4【答案】.C[解析]离心率=,所以===.由双曲线方程知焦点在x轴上,故渐近线方程为y=±x.图1-15.执行如图1-1所示的程序框图,如果输入的t∈[-1,3],则输出的s属于()A.[-3,4]B.[-5,2]C.[-4,3]D.[-2,5]5【答案】.A[解析]由框图可知,当t∈[-1,1)时,s=3t,故此时s∈[-3,3);当t∈[1,3]时,s=4t-t2=-(t-2)2+4,故此时s∈[3,4],综上,s∈[-3,4].12013年普通高等学校招生全国各省市统一考试数学试卷与答案图1-26.如图1-2所示,有一个水平放置的透明无盖的正方体容器,容器高8cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6cm,如果不计容器的厚度,则球的体积为()A.cm3B.cm3C.cm3D.cm36【答案】.A[解析]设球的半径为R,则球的截面圆的半径是4,且球心到该截面的距离是R-2,故R2=(R-2)2+42⇒R=5,所以V=πR3=(cm3).7.设等差数列{an}的前n项和为Sn,若Sm-1=-2,Sm=0,Sm+1=3,则m=()A.3B.4C.5D.67【答案】.C[解析]设首项为a1,公差为d,由题意可知am=Sm-Sm-1=2,am+1=Sm+1-Sm=3,故d=1.又Sm==0,故a1=-am=-2,又Sm=ma1+d=0,∴-2m+=0⇒m=5.8.某几何体的三视图如图1-3所示,则该几何体的体积为()图1-3A.16+8πB.8+8πC.16+16πD.8+16π8【答案】.A[解析]由三视图可知该组合体下半部分是一个半圆柱,上半部分是一个长方体,故体积为V=2×2×4+×π×22×4=16+8π.9.设m为正整数,(x+y)2m展开式的二项式系数的最大值为a,(x+y)2m+1展开式的二项式系数的最大值为b.若13a=7b,则m=()A.5B.6C.7D.89【答案】.B[解析](x+2y)2m展开式的二项式系数的最大值是C,即a=C;(x+2y)2m+1展开式的二项式系数的最大值是C,即b=C, 13a=7b,∴13C=7C,∴13=7,易得m=6.10.已知椭圆E:+=1(a>b>0)的右焦点为F(3,0),过点F的直线交E于A,B两点,若AB的中点坐标为(1,-1),则E的方程为()A.+=1B.+=122013年普通高等学校招生全国各省市统一考试数学试卷与答案C.+=1D.+=110【答案】.D[解析]由题意知kAB=,设A(x1,y1),B(x2,y2),则⇒+=0.由AB的中点是(1,-1)知∴==,联立a2-b2=9,解得a2=18,b2=9,故椭圆E的方程为+=1.11.,已知函数f(x)=若|f(x)|≥ax,则a的取值范围是()A.(-∞,0]B.(-∞,1]C.[-2,1]D.[-2,0]11【答案】.D[解析]方法一:若x≤0,|f(x)|=|-x2+2x|=x2-2x,x=0时,不等式恒成立,x<0时,不等式可变为a≥x-2,而x-2<-2,可得a≥-2;若x>0,|f(x)|=|ln(x+1)|=ln(x+1),由ln(x+1)≥ax,可得a≤恒成立,令h(x)=,则h′(x)=,再令g(x)=-ln(x+1),则g′(x)=<0,故g(x)在(0,+∞)上单调递减,所以g(x)0,a≤0.综上可知,-2≤a≤0,故选D.方法二:数形结合:画出函数|f(x)|=与直线y=ax的图像,如下图,要使|f(x)|≥ax恒成立,只要使直线y=ax的斜率最小时与函...