28.1锐角三角函数(2)VIP免费

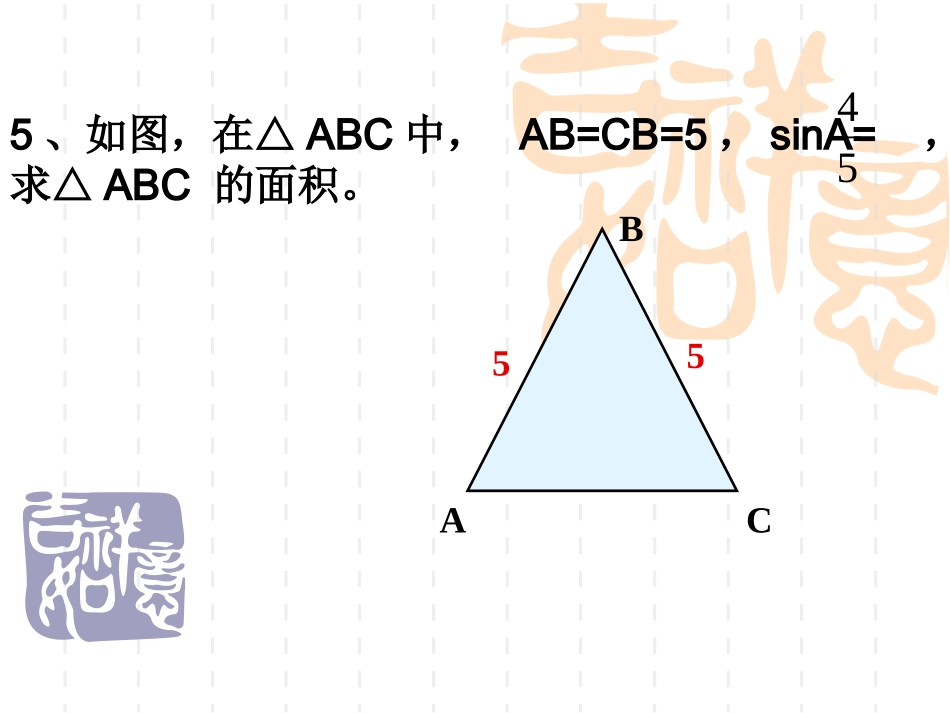
练习2254AC35B2、在平面直角平面坐标系中，已知点A(3，0)和B(0，-4)，则sinOAB∠等于____.3、在RtABC△中，∠C=90°，AD是BC边上的中线，AC=2，BC=4，则sinDAC=___.∠4、在RtABC△中,C=90°∠,,则sinA=___.∠33ba1、如图，求sinA和sinB的值．5、如图，在△ABC中，AB=CB=5，sinA=，求△ABC的面积。54BAC55复习与探究：1.锐角正弦的定义在中，RtABCC90ABCabc∠A的正弦：caABBC斜边A的对边sinA2、当锐角A确定时，∠A的对边与斜边的比就随之确定。此时，其他边之间的比是否也随之确定？为什么？28.1锐角三角函数（2）——余弦正切学习目标1、掌握余弦、正切的概念2、会计算余弦、正切的值新知探索:ABCabc1、你能将“其他边之比”用比例的式子表示出来吗？这样的比有多少？cbba2、当锐角A确定时，∠A的邻边与斜边的比，∠A的对边与邻边的比也随之确定吗？为什么？交流并说出理由。方法一：从特殊到一般，仿照正弦的研究过程；方法二：根据相似三角形的性质来说明。如图，在Rt△ABC中，∠C＝90°，cbAA斜边的邻边cosABC斜边c对边a邻边b★我们把锐角A的邻边与斜边的比叫做∠A的余弦（cosine），记作cosA，即★我们把锐角A的对边与邻边的比叫做∠A的正切（tangent），记作tanA，即baAAA的邻边的对边tanrldmm8989889注意cosA，tanA是一个完整的符号，它表示∠A的余弦、正切，记号里习惯省去角的符号“∠”；cosA，tanA没有单位，它表示一个比值，即直角三角形中∠A的邻边与斜边的比、对边与邻边的比；cosA不表示“cos”乘以“A”，tanA不表示“tan”乘以“A”rldmm8989889对于锐角A的每一个确定的值，sinA有唯一确定的值与它对应，所以sinA是A的函数。同样地，cosA，tanA也是A的函数。cbAA斜边的邻边cosbaAAA的邻边的对边tancaAA斜边的对边sin锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数.rldmm8989889ABC6.34tan54cos,8610.10356sinsin2222BCACBABACABCABACABCABABBCA，又，解：例1如图，在Rt△ABC中，∠C＝90°，BC=6，，求cosA和tanB的值．53sinArldmm8989889例2如图，在Rt△ABC中，∠C＝90°，BC=2，AB=3，求∠A，∠B的正弦、余弦、正切值．.25tan32cos35sin.55252tan35cos32sin,5232222BCACBABBCBABACBACBCAABACAABBCABCABACABCRt，，，，中，解：在ABC23延伸：由上面的计算，你能猜想∠A，∠B的正弦、余弦值有什么规律吗？结论：一个锐角的正弦等于它余角的余弦，或一个锐角的余弦等于它余角的正弦。rldmm8989889练习课本P78练习1，2，3.补充练习1、在等腰△ABC中，AB=AC=5，BC=6，求sinB，cosB，tanB.ABCDrldmm8989889补充练习2、如图所示，在△ABC中，∠ACB＝90°，AC=12，AB=13，∠BCM=BAC∠，求sinBAC∠和点B到直线MC的距离．MCBA3、如图所示，CD是RtABC△的斜边AB上的高，求证：.2BDABBCDCBA