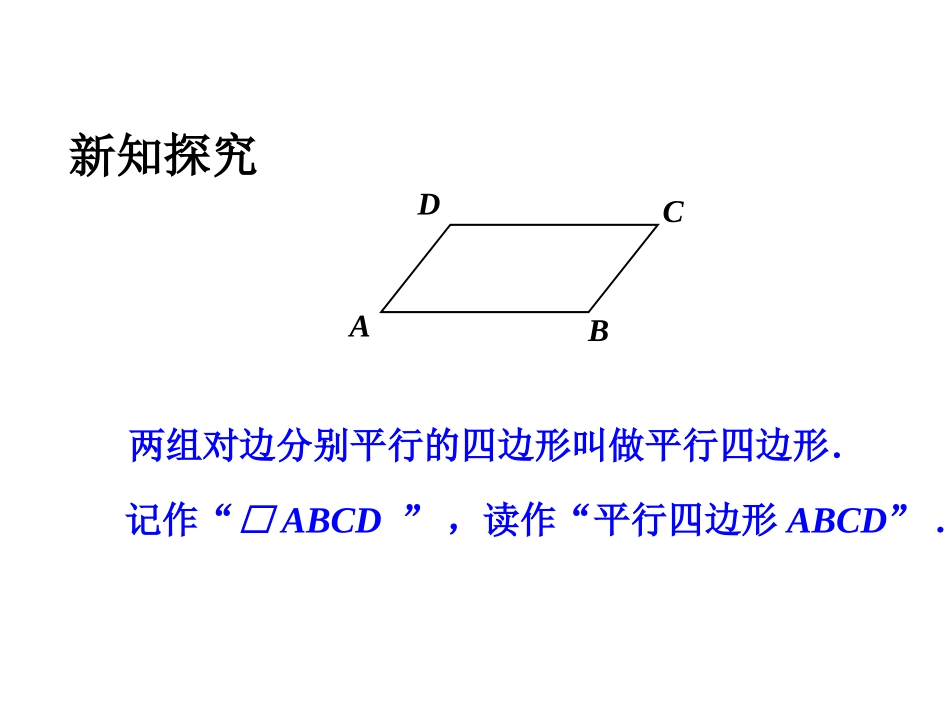
9.3平行四边形(1)下面的图片中,有你熟悉的哪些图形?ADCB两组对边分别平行的四边形叫做平行四边形.记作“□ABCD”,读作“平行四边形ABCD”.新知探究操作思考O是□ABCD对角线AC的中点.用透明纸覆盖在下图,描出□ABCD及其对角线AC,再用大头针钉在点O处,将透明纸上的□ABCD旋转1800.你有什么发现?平行四边形是中心对称图形,对角线的交点是它的对称中心.平行四边形ABCD绕点O旋转180:因为O是AC的中点,所以点A与点C重合,点C与点A重合;因为AB∥CD,可知∠1=∠2,所以AB落在射线CD上;因为AD∥BC,可知∠3=∠4,所以CB落在射线AD上.因为两条直线相交只有一个交点,所以点B(AB和CB的交点)与点D(CD和AD的交点)重合.同理,点D与点B重合.连接BD,因为点B与点D关于点O对称,所以BD经过点O,且被点O平分(如图).思考:从证实□ABCD是中心对称图形的过程中,你发现平行四边形还有哪些性质?平行四边形的对边相等、对角相等、对角线互相平分.ADCBO平行四边形的性质:对称性平行四边形是中心对称图形,对角线的交点是它的对称中心边平行四边形的对角相等;邻角互补。角平行四边形的对边平行且相等;ABCD对角线平行四边形的对角线互相平分。ABCD平行四边形的性质(数学表达式)平行四边形的对边平行且相等;∵四边形ABCD是∴ABCD∥,ADBC∥AB=CD,AD=BC平行四边形的对角相等;邻角互补边角∵四边形ABCD是∴∠A=C,B=D,∠∠∠∠A+C=∠1800,∠B+D=180∠0对角线平行四边形的对角线互相平分。∵四边形ABCD是∴OA=OC,OB=OD例题已知:如图,点A、B、C分别在△EFD的各边上,且AB//DE,BC//EF,CA//FD.求证:A、B、C分别是△EFD各边的中点.F证明:∵CA∥FD,BC∥EF,∴四边形AFBC是平行四边形(两组对边分别平行的四边形是平行四边形)∴AF=BC(平行四边形的对边相等).∴AB∥DE,BC∥EF,∴四边形ABCE是平行四边形(两组对边分别平行的四边形是平行四边形).∴AE=BC(平行四边形的对边相等).∴AF=AE.同理BD=BF,CD=CE.∴A、B、C分别是△DEF各边的中点.思考:△ABC和△EFD的内角分别相等吗?为什么?你还能得到哪些结论?证明你的结论.解:△ABC与△DEF的内角分别相等,即∠BAC=∠D,∠ACB=∠F,∠ABC=∠E.理由:∵AB∥DE,BC∥EF,∴四边形ABCE是平行四边形,∴∠ABC=∠E.同理可证∠BAC=∠D,∠ACB=∠F.图中AF=AE=BC,AB=CD=CE,AC=BD=BF.理由:∵四边形AFBC是平行四边形,∴AF=BC.又∵四边形ABCE是平行四边形,∴BC=AE,∴AF=AE=BC.同理可证AB=CD=CE,AC=BD=BF.基础训练2.在□ABCD中,已知∠A=80°,那么∠B=,C=∠,D=∠;1.下列特征中,平行四边形不一定具是()A.对角互补B.邻角互补C.一组对边相等D.内角和是360°A100°80°100°4.在□ABCD中,已知∠A﹕B=13∠﹕,那么∠C=,D=∠;3.在□ABCD中,已知∠A+C=140°∠,那么∠A=,B=∠,C=∠;70°110°70°45°135°5.在□ABCD中,已知∠A=2B∠,那么∠A=,B=∠;6.在□ABCD中,已知∠A-B=70°∠,那么∠A=C=∠,B=D=∠∠;120°60°125°55°7.如图,在□ABCD中,∠D=72°,BE平分∠ABC,则∠ABE=;72°EDCBA36°8.若□ABCD的周长为36cm,AB=8cm,则BC=cm,CD=cm;9.若□ABCD的周长为44cm,AB比BC短2cm,则AB=CD=cm,则BC==cm;10810AD12ABDCE9cm5cm10.如图所示,在□ABCD中,若BE平分∠ABC,则ED=.4cm235cm5cm4cm111.如图,在□ABCD中,AC=24,BD=40,AD=30,则AO=,BOC△的周长=;ADBCO126212.若平行四边形的两条对角线长分别是8cm和10cm,则平行四边形的边长可以是()A.1cmB.8cmC.10cmD.18cmB13.如图,直线EF过平行四边形ABCD对角线的交点O,分别交AB、CD于E、F,那么阴影部分的面积是平行四边形ABCD面积的()A.B.C.D.OFEDCBA514131103B拓展延伸如图:□ABCD的周长是36,由钝角顶点D向AB、BC引两条高DE、DF,且DE=4,DF=6,求这个平行四边形的面积.ECBFAD从平行四边形的一个锐角的顶点做两条高线,如果这两条高线的夹角是135°,求这个平行四边形的锐角的度数.45°14.如图所示,□ABCD的周长为36cm,AB﹕BC=12,BC=12﹕∠﹕∠﹕,E是BC边的中点,求AE的长;EDCBA这节课学习了什么?有什么收获?