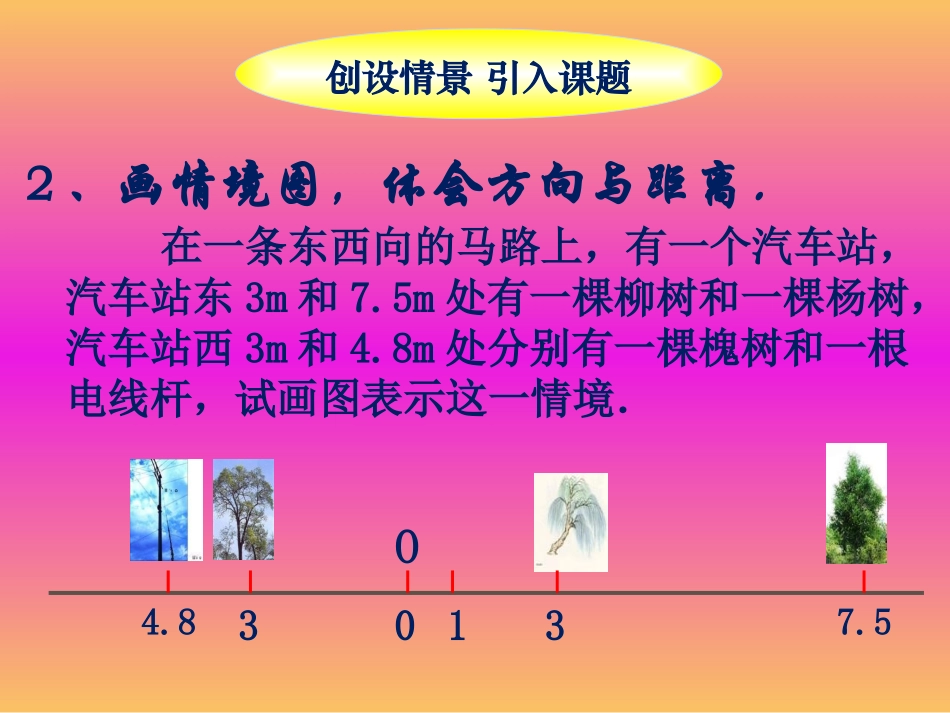
1.2.2数轴1、观察温度计,体会数、形对应.创设情景引入课题学生观察温度计后回答下列问题:-10-5051015202530-10-5051015202530-10-5051015202530①零上5℃怎样表示?②零下10℃怎样表示?③0℃怎样表示?创设情景引入课题2、画情境图,体会方向与距离.在一条东西向的马路上,有一个汽车站,汽车站东3m和7.5m处有一棵柳树和一棵杨树,汽车站西3m和4.8m处分别有一棵槐树和一根电线杆,试画图表示这一情境.O0137.534.8创设情景引入课题3、对比观察,引入课题.O0137.534.8-10-5051015202530-10-5051015202530-10-5051015202530得出定义揭示内涵1、提问,到底什么是数轴?如何画数轴?0123-1-2-3原点正方向(向左或向右)单位长度2、丰富数轴的内涵:分数和小数在数轴上怎么表示?0123-1-2原点正方向(向左或向右)单位长度25211.5得出定义揭示内涵①位于数轴左(下)边的数总比右(上)边的数小.②一般地,设a是一个正数,则数轴上表示数a在原点的____边,与原点的距离是____个单位长度;表示数-a的点在原点的____边,与原点的距离是____个单位长度.3、观察数轴上的有理数排列的大小?0123-1-2-3手脑并用深入理解A11、学生讨论下列图形中哪些是数轴,哪些不是,为什么?B102-1D0-212E1212-1-1-2-20xyC0-123-1手脑并用深入理解3、指出数轴上A、B、C、D、E点分别表示什么数?1234560-1-2-3-4-5ABCDE1.5,-2,2,0,,2932-2、画数轴并表示出下列有理数.归纳总结强化思想1、你知道什么是数轴吗?这节课你学会了用什么来表示有理数?2、数轴上,会不会有两个点表示同一个有理数?会不会有一个点表示两个不同的有理数?1、教材第10页第1、2题.在数轴上能否实际画出表示一千分之一的点?这个点存在吗?2、思考练习作业布置