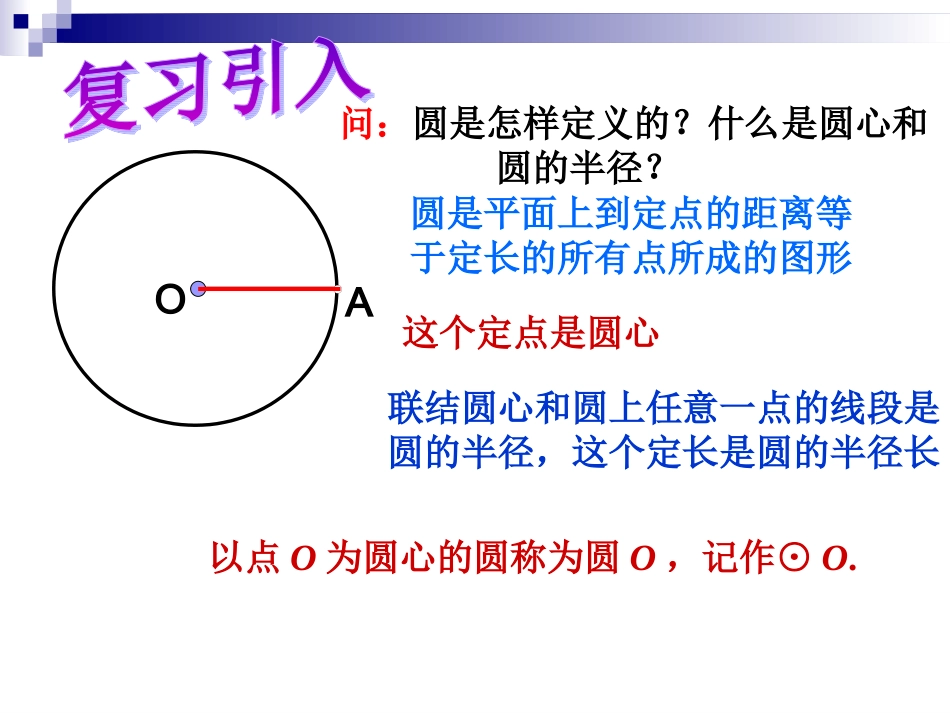
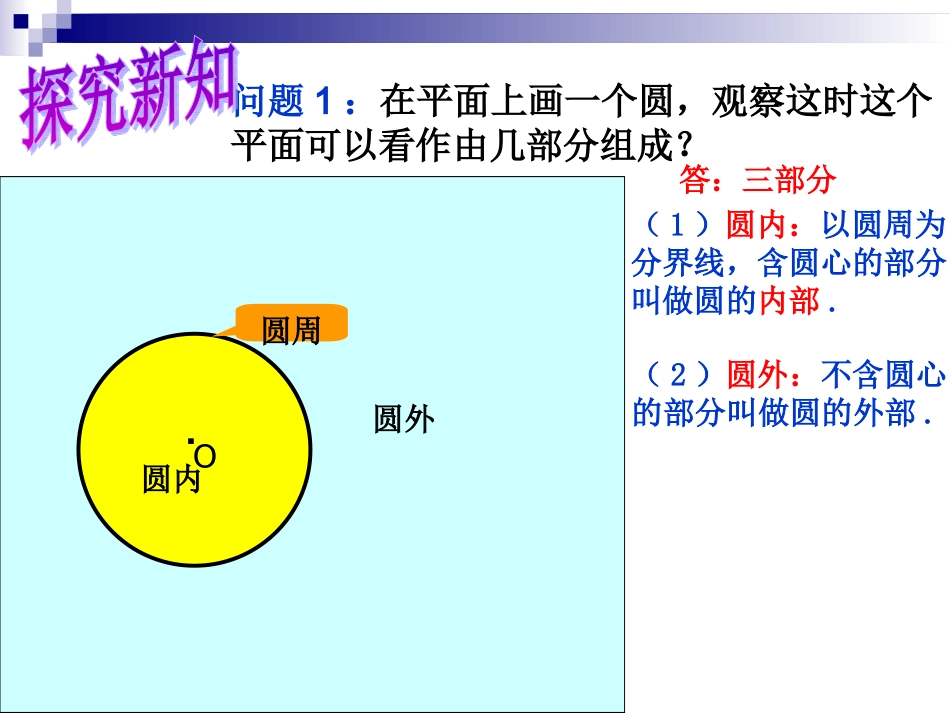
AO圆是平面上到定点的距离等于定长的所有点所成的图形这个定点是圆心联结圆心和圆上任意一点的线段是圆的半径,这个定长是圆的半径长以点O为圆心的圆称为圆O,记作⊙O.问:圆是怎样定义的?什么是圆心和圆的半径?问题1:在平面上画一个圆,观察这时这个平面可以看作由几部分组成?·O圆内圆外圆周答:三部分(1)圆内:以圆周为分界线,含圆心的部分叫做圆的内部.(2)圆外:不含圆心的部分叫做圆的外部.M····OABC问题2:(1)观察图中点A,点B,点C与圆的位置关系?答:点A在圆内,点B在圆上,点C在圆外(2)设⊙O半径为r,说出点A,点B,点C到圆心O的距离与半径的数量关系rOAr.····OP1P2P3设⊙O的半径长为R,点P到圆心的距离为d,则点P在圆外d>R点P在圆上d=R点P在圆内dAB。得BC>AC。∵AC是⊙C的半径,∴点B在⊙C外。2121ACB图1rdCAB图2rd······ABA问题2:如图作经过已知点A、B的圆,这样的圆你能作出多少个?这些圆的圆心分布有什么特点?问题1:经过一点A作圆,能作多少个?答:无数多个答:无数多个这些圆的圆心都在线段AB的垂直平分线上.问题3:过平面上的三点A、B、C能否画一个圆?l1l2ABC过平面上共线的三点不能画一个圆.问:过平面上不共线的三点能否画一个圆?GDOFECBAO答:能问:其圆心在什么位置?经过A、B两点的圆的圆心在线段AB的垂直平分线上.经过B、C两点的圆的圆心在线段BC的垂直平分线上.经过A、B、C三点的圆的圆心在这两条垂直平分线的交点O的位置.定理:不在同一条直线上的三个点确定一个圆.外接圆的圆心是三角形三条边垂直平分线的交点,叫做这个三角形的外心.COAB经过三角形的三个顶点可以做一个圆,这个圆叫做三角形的外接圆,这个三角形叫做这个圆的内接三角形.如图,⊙O是△ABC的外接圆,△ABC是⊙O的三角形ABCD如果一个圆经过一个多边形的各顶点,那么这个圆叫做这个多边形的外接圆,这个多边形叫做这个圆的内接多边形.如图,⊙O是四边形ABCD的外接圆,四边形ABCD是⊙O的内接四边形.例题2:已知钝角三角形ABC,用直尺和圆规作出这个三角形的外接圆ABC1l2lDEO1l1.作线段AB的垂直平分线2l2.作线段AC的垂直平分线1l2l设和相交于点O.O作法:以点O为圆心,OA为半径作⊙O,⊙O就是所求作的圆.问:在Rt△ABC中,∠C=90°,它的外接圆的圆心在什么地方?为什么?BAC┐●O因为斜边上的中线等于斜边的一半,即斜边的中点到直角三角形三个顶点的距离相等.所以,直角三角形外接圆的圆心在斜边上,就是斜边的中点.直角三角形外接圆的圆心在斜边上,就是斜边的中点.不同类型的三角形外心的位置特征:锐角三角形的外心位于三角形内,直角三角形的外心位于直角三角形斜边中点,钝角三角形的外心位于三角形外.ABC●OABCCAB┐●O●O1、按图填空:(1)△ABC是⊙O的_________三角形.(2)⊙O是△ABC的_________圆.(3)点O是△ABC的________心.(4)OA、OB、OC的长度有关系:____________.内接外接外OA=OB=OCABCO2.判断题:(1)经过三点一定可以作圆.()(2)三角形的外心就是这个三角形两边垂直平分线的交点。()(3)三角形的外心到三边的距离相等。()(4)任意一个三角形一定有一个外接圆,并且只有一个外接圆.()(5)任意一个圆一定有一个内接三角形,并且只有一个内接三角形.()不共线三点×√×三个顶点√×无数个ABCD3.经过不在同一直线上的任意四点,是否一定可以作一个圆?举例说明.不一定过已知正方形四个顶点可以作一个圆,但过已知菱形四个顶点不可以作一个圆.ABCDABCDABCD2.点与圆的位置关系;1.不共线的三点可以确定一个圆;点在圆内;点在圆外.点在圆上;GDOFECBAO····OABC3.不同类型的三角形外心的位置.ABC●OCAB┐●OABC●O练习册习题27.1