动量守恒定律的综合应用VIP免费

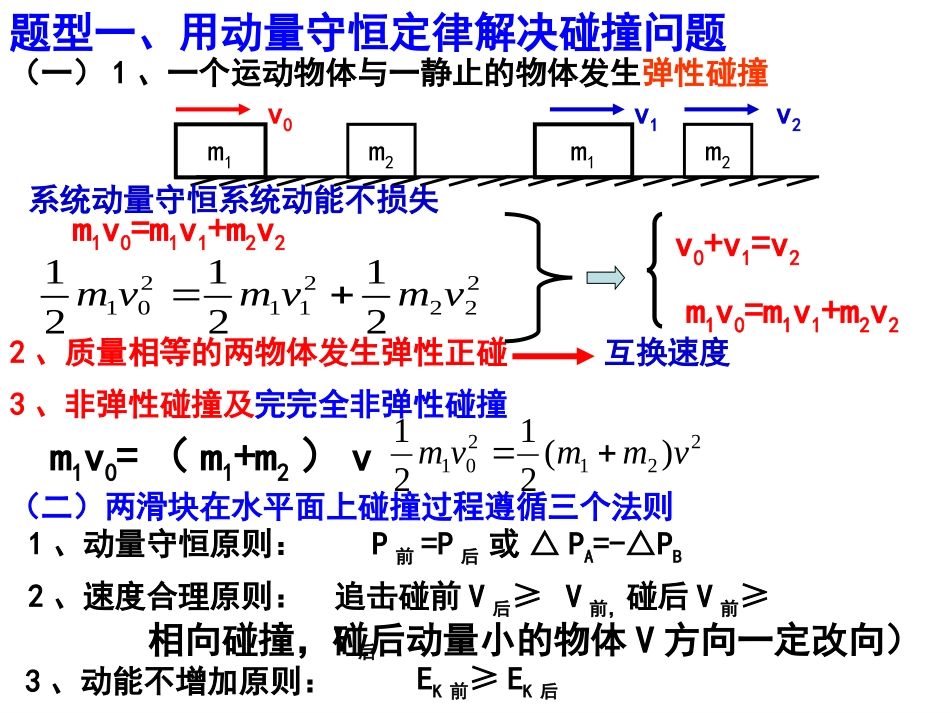
动量守恒定律的综合应用题型一、用动量守恒定律解决碰撞问题1、动量守恒原则：2、速度合理原则：3、动能不增加原则：P前=P后或△PA=-△PBEK前≥EK后追击碰前V后≥V前，碰后V前≥V后相向碰撞，碰后动量小的物体V方向一定改向）（二）两滑块在水平面上碰撞过程遵循三个法则（一）1、一个运动物体与一静止的物体发生弹性碰撞m1m2v0m1m2v1v2系统动量守恒系统动能不损失m1v0=m1v1+m2v2222211201212121vmvmvm2、质量相等的两物体发生弹性正碰互换速度3、非弹性碰撞及完完全非弹性碰撞m1v0=（m1+m2）v221201)(2121vmmvmm1v0=m1v1+m2v2v0+v1=v2例1如图3所示，一个质量为m的小球A被长为L的轻质细绳悬挂，小球A可以绕悬点O在竖直平面内摆动，开始时小球A静止且恰能与桌面边缘接触而不发生相互作用．在光滑水平桌面上，另一个质量为2m的小球B以某一初速度向右运动与小球A发生正碰，碰撞中无机械能损失．两小球大小形状完全相同，均可看成质点，已知m＝1kg、L＝1m、悬点O到右侧竖直墙壁的水平距离s＝0.8m，轻质细绳能够承受的最大拉力为50N，重力加速度g取10m/s2，水平桌面离地面足够高，不计空气阻力．求：(1)当小球B的初速度v1＝3m/s时，小球A将要与墙壁发生碰撞时速度大小；(2)当小球B的初速度v2＝6m/s时，小球A、B与墙壁分别发生碰撞的位置之间的距离．解析(1)当小球B的初速度v1＝3m/s时，小球B与小球A发生正碰，系统动量守恒：2mv1＝2mvB1＋mvA1系统机械能守恒：12×2mv12＝12×2mvB12＋12mvA12解得：vA1＝4m/s，vB1＝1m/s碰后对小球A受力分析得：F－mg＝mvA12L解得：F＝26NF<50N，悬线未拉断，小球A在竖直平面内绕悬点O向上摆动，当小球A将要与墙壁发生碰撞时，据机械能守恒定律得：mgh＝12mvA12－12mvA2根据几何关系得：L2＝(L－h)2＋s2解得：vA＝22m/s＝2.83m/s(2)当小球B的初速度v2＝6m/s时，小球B与小球A发生正碰，系统动量守恒：2mv2＝2mvB2＋mvA2系统机械能守恒：12×2mv22＝12×2mvB22＋12mvA22解得：vA2＝8m/s，vB2＝2m/s碰后对小球A受力分析得：F－mg＝mvA22L解得：F＝74N>50N，悬线拉断．小球A平抛运动：s＝vA2t1，hA＝12gt12小球B平抛运动：s＝vB2t2，hB＝12gt22Δh＝hB－hA，联立解得：Δh＝0.75m.变式题：跟踪训练2．(2010·山东高考)如图4－2所示，滑块A、C质量均为m，滑块B质量为32m.开始时A、B分别以v1、v2的速度沿光滑水平轨道向固定在右侧的挡板运动，现将C无初速地放在A上，并与A粘合不再分开，此时A与B相距较近，B与挡板相距足够远．若B与挡板碰撞将以原速率反弹，A与B碰撞将粘合在一起．为使B能与挡板碰撞两次，v1、v2应满足什么关系？解析：设向右为正方向，A与C粘合在一起的共同速度为v′，由动量守恒定律得mv1＝2mv′①为保证B碰挡板前A未能追上B，应满足v′≤v2②设A与B碰后的共同速度为v″，由动量守恒定律得2mv′－32mv2＝72mv″③为使B能与挡板再次碰撞应满足v″>0④联立①②③④式得1．5v2