2015年第一章-第二节-30°-45°-60°角的三角函数值VIP免费

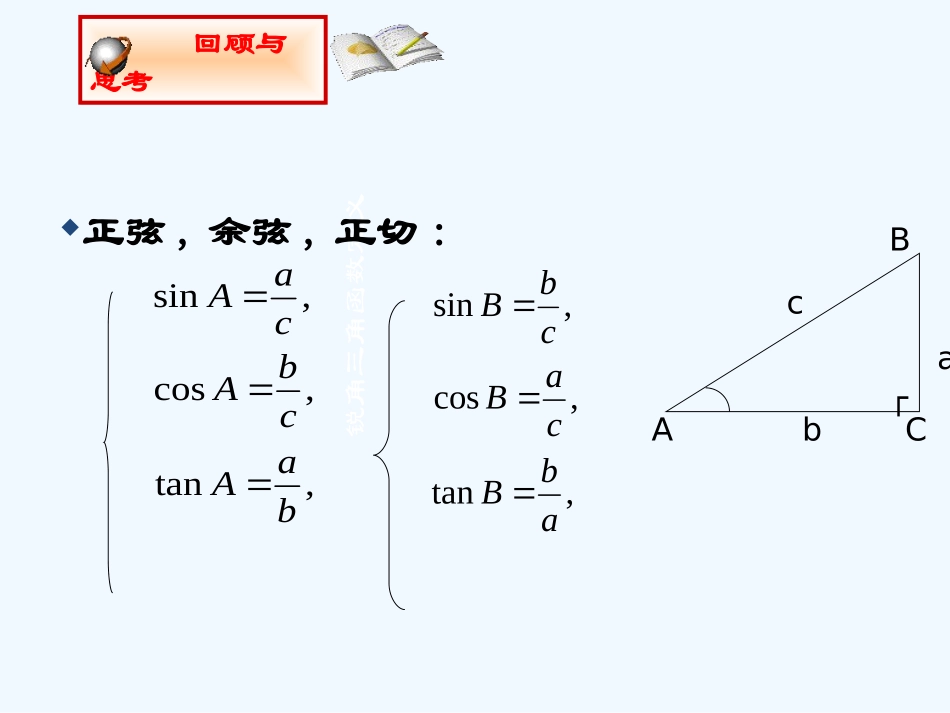
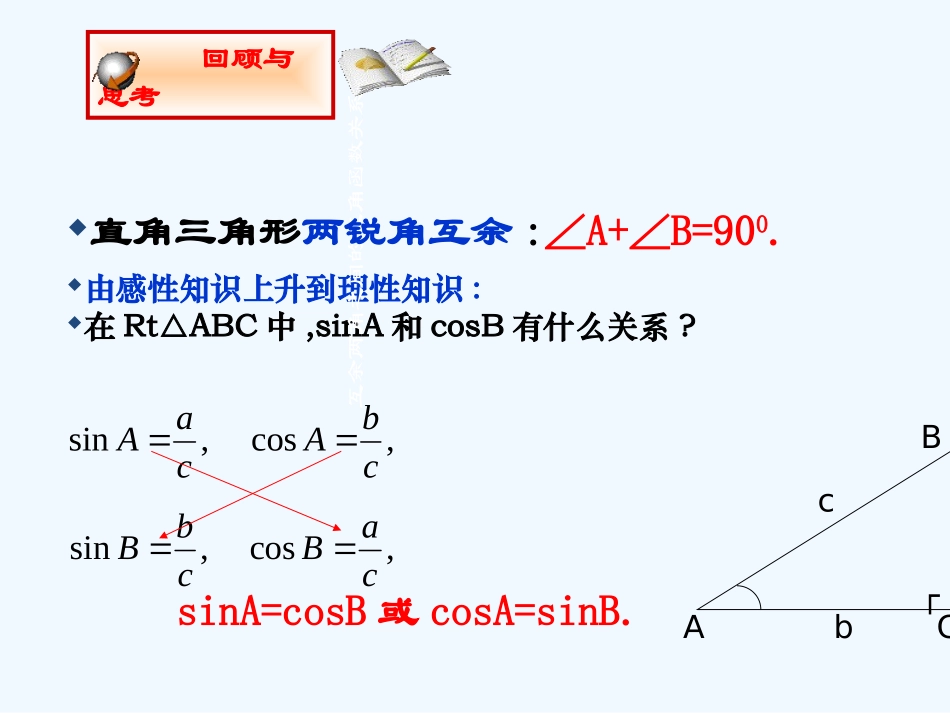
北师大版九年级（下）230°,45°,600°角的三角函数值锐角三角函数定义正弦,余弦,正切:回顾与思考bABCa┌c,sincaA,coscbA,tanbaA,sincbB,coscaB,tanabB由感性知识上升到理性知识:在Rt△ABC中,sinA和cosB有什么关系?互余两角之间的三角函数关系直角三角形两锐角互余:∠A+∠B=900.回顾与思考bABC┌csinA=cosB或cosA=sinB.,sincaA,coscbA,sincbB,coscaB一个锐角的正弦,等于它的余角的余弦(或一个锐角的余弦等于它的余角的正弦);互余两角之间的三角函数关系结合图形,将sinA=cosB或cosA=sinB用文字语言叙述出来:回顾与思考bABC┌c,sincaA,coscbA,sincbB,coscaB一个锐角的正弦,等于它的余角的余弦(或一个锐角的余弦等于它的余角的正弦);互余两角之间的三角函数关系一般地,∠α的余角为900-∠α,即∠α和900-∠α角互为余角.回顾与思考:因此更一般地有,cos90sin0,sin90cos0本领大不大悟心来当家如图,观察一副三角板:它们其中有几个锐角?分别是多少度?想一想(1)sin300等于多少?┌┌300600450450(2)cos300等于多少?(3)tan300等于多少?请与同伴交流你是怎么想的?又是怎么做的?1不仿设两个三角形最短的边长为单位1,易得:11232知识在于积累(5)sin450,sin600等于多少?做一做(6)cos450,cos600等于多少?(7)tan450,tan600等于多少?根据上面的计算,完成下表:<特殊角的三角函数值表>老师期望:你能对伴随九个学年的这副三角尺所具有的功能来个重新认识和评价.┌┌300600450450111232洞察力与内秀特殊角的三角函数值表做一做要能记住有多好三角函数锐角α正弦sinα余弦cosα正切tanα3004506002123332222123213这张表还可以看出许多知识之间的内在联系呢?行家看“门道”例1计算:(1)sin300+cos450;(2)sin2600+cos2600+tan450.例题欣赏老师提示:Sin2600表示(sin600)2,cos2600表示(cos600)2,其余类推.解:(1)sin300+cos450(2)sin2600+cos2600-tan4502221.221121232214143.0知识的运用(1)sin600-cos450;(2)cos600+tan600;随堂练习计算:.45cos260sin45sin223000老师期望:只要勇敢地走向黑板来展示自己,就是英雄!.45cos260cos30sin224020202223232122231862真知在实践中诞生例2如图:一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰好为600,且两边摆动的角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01m).便是欣赏老师提示:将实际问题数学化.真知在实践中诞生实际问题数学化:便是欣赏咋办∴最高位置与最低位置的高度差约为0.34m.,5.2,30602100OAOBAOBACOBD┌解:如图,根据题意可知,,30cos0OBOC∴AC=OA-OC=2.5-2.165≈0.34(m).).(165.2235.230cos0mOBOC●2.5老师期望:sin2A+cos2A=1它反映了同角之间的三角函数的关系,且它更具有灵活变换的特点,若能予以掌握,则将有益于智力开发.八仙过海,尽显才能2.某商场有一自动扶梯,其倾斜角为300,高为7m,扶梯的长度是多少?随堂练习3.如图,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c.求证:sin2A+cos2A=1bABCa┌c灵活变换:同角之间的三角函数的关系3.如图,在Rt△ABC中,∠C=900,∠A,∠B,∠C的对边分别是a,b,c.求证:sin2A+cos2A=1随堂练习bABC┌c,,cos,sin:222cbacbAcaA证明2222cossincbcaAA222cba22cc.1.1cossin22AA即.cos1sin22AA.sin1cos22AA.cos1sin2AA或.sin1cos2AA或同角之间的三角函数的关系3.如图,在Rt△ABC中,∠C=900,∠A,∠B,∠C的对边分别是a,b,c.求证:随堂练习bABC┌c,tan:baA证明.tancossinAbacbcaAA.cossintanAAA,cos,sincbAcaA同角之间的三角函数的关系平方和关系:随堂练习bABCa┌c.1cossin22AA.cos1sin22AA.cos1sin2AA或.sin1cos22AA.sin1cos2AA或商的关系:.cossintanAAA•直角三角形中的边角关系小结拓展看图说话:直角...