122同角三角函数的基本关系VIP免费

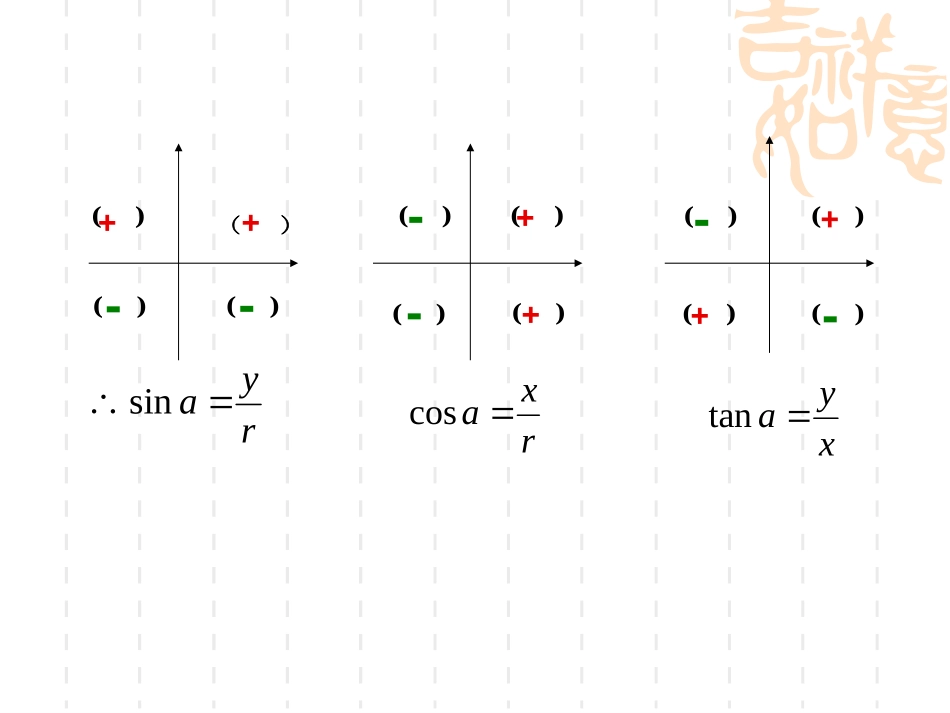
三角函数1.2.2同角三角函数的基本关系（第1课时）ryasinrxacosxyatan()()()()()()()()()()()（）++--++--++--终边相同{|2,}kkz)(tan)2tan(cos)2cos(sin)2sin(zkkkk终边相同的角的集合点的坐标相同同一函数值相同公式一sin(292360)sin29公式一：判断下列式子的正误cos(1573180)cos157tan(483360)tan(48)cos(483360)sin(48)sin(4)sin()44cos(3)cos()44tan(6)tan()44归纳探索304560150sincostan123233222213212312323322sincossincos22sincos1sintancos1111331333基本关系22rxyyxO(,)Pxyrcosxrsinyαrtanyx22sincos1sintancos同角公式22sincos122sin1cos22cos1sin2sin1cos2cos1sin同角三角函数的基本关系平方关系:商数关系:1cossin22cossintan),2(Zkk同一个角的正弦、余弦的平方和等于1，商等于角的正切.“同角”二层含义:一是”角相同”,二是”任意”一个角.知识探究：基本变形思考1：对于平方关系可作哪些变形？22sincos122sin1cos,22cos1sin,2(sincos)12sincos,aaaa+=+2(sincos)12sincos,aaaa-=-思考2：对于商数关系可作哪些变形？sintancossincostan,aaa=×sincos.tan注意注意“同角”，至于角的形式无关重要，;13cos3sin:22如.23tan23cos23sin.259541sin1cos222从而.343554cossintan54sin已知,且是第二象限角,求的值.tan,cos例1解：54sin由1cossin22得.53259cos因为是第二象限角,那么0cos例2：已知，求的值。3sin5cos,tan解：3sin05IIIIV或（1）当时IIIcos024cos1sin5sin3tancos4（2）当时IVcos024cos1sin5sin3tancos4分类讨论练习:已知，求的值。3tan4sin,cos解：3tan04yxIIII或（1）当时I0,0xy3sin5yr不妨设x=4，y=3225rxy4cos5xr（2）当时III0,0xy3sin5yr不妨设x=-4，y=-3225rxy4cos5xr分类讨论例3：求证xxxxcossin1sin1cos法一（作差）0sin1cossin1sin1coscossin1sin1cos2xxxxxxxxx法二：综合分析法xxxxxxcoscoscossin1sin1sin1220sin1x0cosx且xxxxcossin1sin1cos法三：0cosx1sinx0sin1x左边xxxxxxxxxcossin1sin1sin1cossin1sin1sin1cos2右边tancos,23sin)1(、求是第四象限的角且已知cossin43tan)3(、求tancos31sin)2(和求课堂练习：（4）化简tancos①②③22costan122sin211cos2化简的基本要求1.项数最少、次数最低、函数种类最少;2.分母不含根号,能求值的要求值.2244cossincossin:)5(证明tan1tan1sincoscossin2122xx1coscossinsin22244433cossincossintan1tancossin2cossin求（6）计算同角公式的应用P25B3sincostan2sincos已知求解：分子分母同时除以coscosαα得：得：sincossincoscossincossincoscossincoscoscossincoscoscostan1tan121321sintancos分析：练习2sin3costan3sin4cos(1)已知求221tan3sincos(2)已知求22tan3sin3cos(3)2已知求22cossin1换为1小结2.已知tanα，求sinα，cosα22sincos122sin1cos22cos1sin2sin1cos2cos1sin1.已知sinα（或cosα）求其它sintancostanyx3.注意分象限讨论小结:2.同角三角函数关系的基本关系的应用1.通过观察、归纳,发现同角三角函数的基本关系.发现规律(2)公式的变形、化简、恒等式的证明.规律的应用(1)已知角的某一三角函数值,求它的其它三角函数值;