1.2充分条件与必要条件（通用） (2)VIP免费

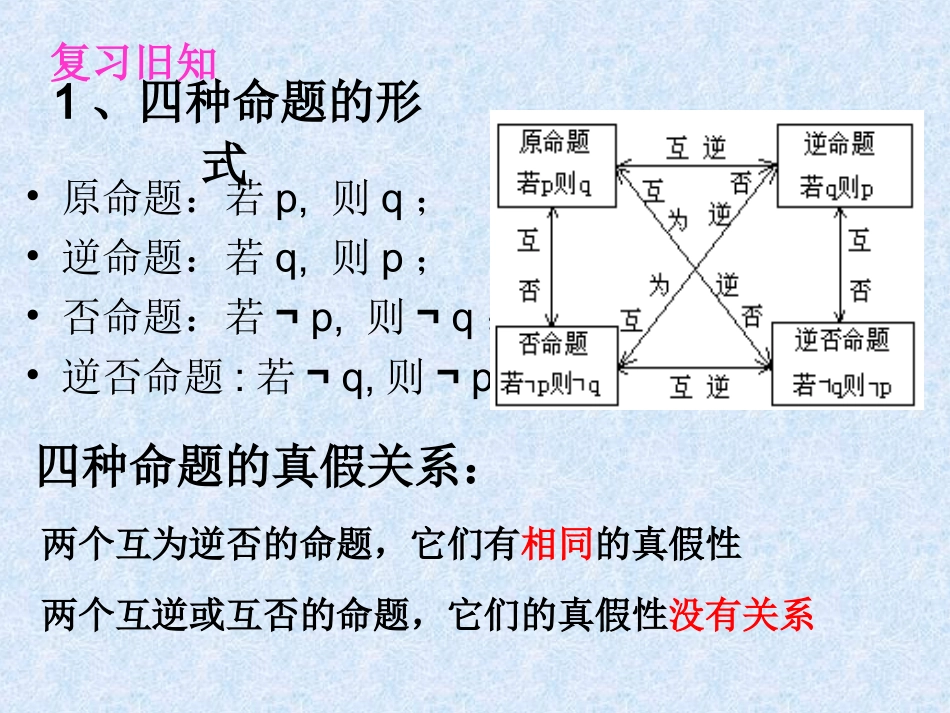
滨海新区大港油田一中滨海新区大港油田一中宋艳东宋艳东1、四种命题的形式•原命题：若p,则q；•逆命题：若q,则p；•否命题：若¬p,则¬q；•逆否命题:若¬q,则¬p.复习旧知四种命题的真假关系：两个互为逆否的命题，它们有相同的真假性两个互逆或互否的命题，它们的真假性没有关系一般地,如果p⇒q,那么称p是q的________,同时称q是p的________.充分条件必要条件复习旧知2、充分、必要条件定义一般地,如果既有pq,⇒又有qp,⇒那么称p是q的充分必要条件,简称_____________.当p是q的充要条件时，常记作________，或表示p与q________.充要条件pq⇔等价3、充要条件定义复习旧知若，且，则p是q的必要不充分条件；pqpq若，且，则p是q的充要条件pqpq充分、必要条件的分类若，且，则p是q的既不充分也不必要条件.pqpqpq若，且，则p是q的充分不必要条件；pq条件：p结论：q结论p,q的逻辑关系集合A,B的关系韦恩图示p是q的充分不必要条件pq且pqABp是q的必要不充分条件pq且pqBAp是q的充要条件pq且pqABp是q的既不充分也不必要条件pq且pqAB且BABAABBA建立与p､q相应的集合,即条件p:A={x|p(x)},结论q:B={x|q(x)}.A(B)AB解题方法步骤：（2）考察条件和结论间的相互推出关系；（1）分清条件是什么和结论是什么；口诀：条推结充分性，结推条必要性反思：解决这一类问题的方法步骤是什么？（3）根据定义作出判断，确定条件是结论的什么条件。若条件结论为充分性，若条件结论为不充分；若结论条件为必要性；若结论条件为不必要。⇒⇒强调：小范围⇒大范围，大范围小范围例1若a∈R，命题p:“a＝1”，命题q：“|a|＝1”。则q是p的()条件A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件B分析：确定谁是条件谁是结论分析：确定谁是条件谁是结论结论是结论是p：a=1条件是条件是q：|a|＝1化简为a=1或a=-1考点一充分条件、必要条件的基本应用a=1或a=-1a=1例2.(2016·天津卷)设x>0，y∈R，则“x>y”是“x>|y|”的()A.充要条件B.充分不必要条件C.必要不充分条件D.既不充分也不必要条件解析x>yx>|y|(如x＝1，y＝－2).但x>|y|时，能有x>y.答案C考点一充分条件、必要条件的基本应用条件条件：x>y结论结论：x>|y|││xx│>1│>1的一个充分不必要条件是的一个充分不必要条件是（（））A.A.xx<<00或或xx>>11；；B.B.xx>>33;;C.C.xx<<-1-1或或xx>>11；；DD..xx<<00；；B分析：分析：①①确定谁是定义中的条件和结论。确定谁是定义中的条件和结论。条件为条件为选项选项结论为结论为││xx│>1│>1例3考点一充分条件、必要条件的基本应用化简为xx<<-1-1或或xx>>11②②利用集合思想解决问题利用集合思想解决问题结论结论xx<<-1-1或或xx>>11条件X>3考点二充分条件、必要条件的应用——含有参数问题【例4】已知P＝{x|x2－8x－20≤0}，非空集合S＝{x|1－m≤x≤1＋m}.若x∈P是x∈S的必要不充分条件，求m的取值范围.解由x2－8x－20≤0，得－2≤x≤10，∴P＝{x|－2≤x≤10}. x∈P是x∈S的必要不充分条件，∴S⇒P且PS，则SP.∴1012111mmmm解得30m.综上，可知0≤m≤3时，x∈P是x∈S的必要不充分条件.解由例题知P＝{x|－2≤x≤10}.若x∈P是x∈S的充要条件，则P＝S，∴1－m＝－2，1＋m＝10，∴m＝3，m＝9，这样的m不存在.考点二充分条件、必要条件的应用——含有参数问题【变式训练1】已知P＝{x|x2－8x－20≤0}，非空集合S＝{x|1－m≤x≤1＋m}.问是否存在实数m，使x∈P是x∈S的充要条件？解由例题知P＝{x|－2≤x≤10}. ¬P是¬S的必要不充分条件，∴¬S⇒¬P且¬P¬S等价于P⇒S且SP.则PS.∴[－2，10][1－m，1＋m].∴10121mm∴m≥9，则m的取值范围是[9，＋∞).【变式训练2】已知P＝{x|x2－8x－20≤0}，非空集合S＝{x|1－m≤x≤1＋m}.若¬P是¬S的必要不充分条件，求实数m的取值范围考点二充分条件、必要条件的应用——含有参数问题规律方法充分条件、必要条件的应用，一般表现在参数问题的求解上.解题时需注意：(1)把充分条件、必要条件或充要条件转化为集...