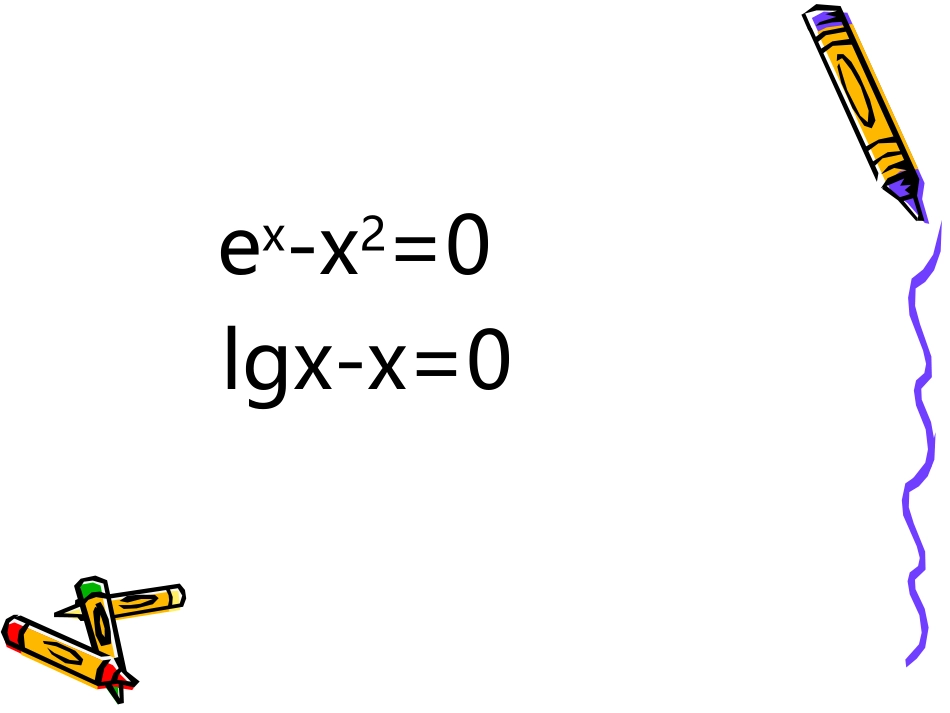1.11.1利用函数性质判定利用函数性质判定方程解的存在方程解的存在1.11.1利用函数性质判定利用函数性质判定方程解的存在方程解的存在第四章函数应用§1函数与方程ex-x2=0lgx-x=0(一)了解函数零点的概念;理解函数零点与方程的根之间的关系;掌握判定函数零点存在的方法;(二)培养学生独立思考,自主观察和探究的能力;树立数形结合,函数与方程相结合的思想;(三)培养学生用联系的观点看待问题;感悟由具体到抽象,由特殊到一般的研究方法,形成严谨的科学态度。学习提纲方程2x+1=0的根与函数y=2x+1的图像与x轴交点坐标有何关系?方程x2-3x+2=0的根与函数y=x2-3x+2的图像与x轴交点坐标有何关系?一般函数与方程也具有该关系吗?判断下列结论是否正确,若不正确,请举出反例:(1)已知函数y=f(x)在区间[a,b]上连续,且f(a)f(b)<0,则f(x)在区间(a,b)内有且仅有一个零点。(2)已知函数y=f(x)在区间[a,b]上连续,且f(a)f(b)>0,则f(x)在区间(a,b)内没有零点。(3)已知函数y=f(x)在区间[a,b]上满足f(a)f(b)<0,则f(x)在区间(a,b)内存在零点。函数的零点我们把函数y=f(x)的图像与横轴的交点的横坐标称为这个函数的零点。方程有实数解f(x)0=xyf(x)=函数的图像与轴有交点函数有零点yf(x)=等价关系:例1函数y=x(x2-16)的零点为()函数的零点与方程的根有什么共同点和区别?判断下列结论是否正确,若不正确,请举出反例:(1)已知函数y=f(x)在区间[a,b]上连续,且f(a)f(b)<0,则f(x)在区间(a,b)内有且仅有一个零点。(2)已知函数y=f(x)在区间[a,b]上连续,且f(a)f(b)>0,则f(x)在区间(a,b)内没有零点。(3)已知函数y=f(x)在区间[a,b]上满足f(a)f(b)<0,则f(x)在区间(a,b)内存在零点。零点存在定理:若函数y=f(x)在区间[a,b]上的图像是连续曲线,并且在区间端点的函数值符号相反,即f(a)·f(b)<0,则在区间(a,b)内,函数y=f(x)至少有一个零点,即相应的方程f(x)=0在区间(a,b)内至少有一个实数解.xxyy00aabb....xxyy00aabbxxyy00aabb......例2.y=ex-x2在[-1,0]内有没有零点?效果检测,能力提升1.求函数f(x)=lnx+2x-6的零点个数2.已知函数f(x)=x2-2ax+a+2,当a为何值时,函数有两个正零点?当a为何值时,函数在(1,3)内有两个不同的零点?当a为何值时,函数有一个大于2,一个小于-2的零点?3.已知函数f(x)=若函数g(x)=f(x)-m有3个零点,则实数m的取值范围是________.0),1(log0,222{xxxxx课堂小结知识:(1)零点的概念(2)零点存在的判定方法(3)利用图像确定零点的个数方法:由特殊到一般思想:数形结合和转化思想