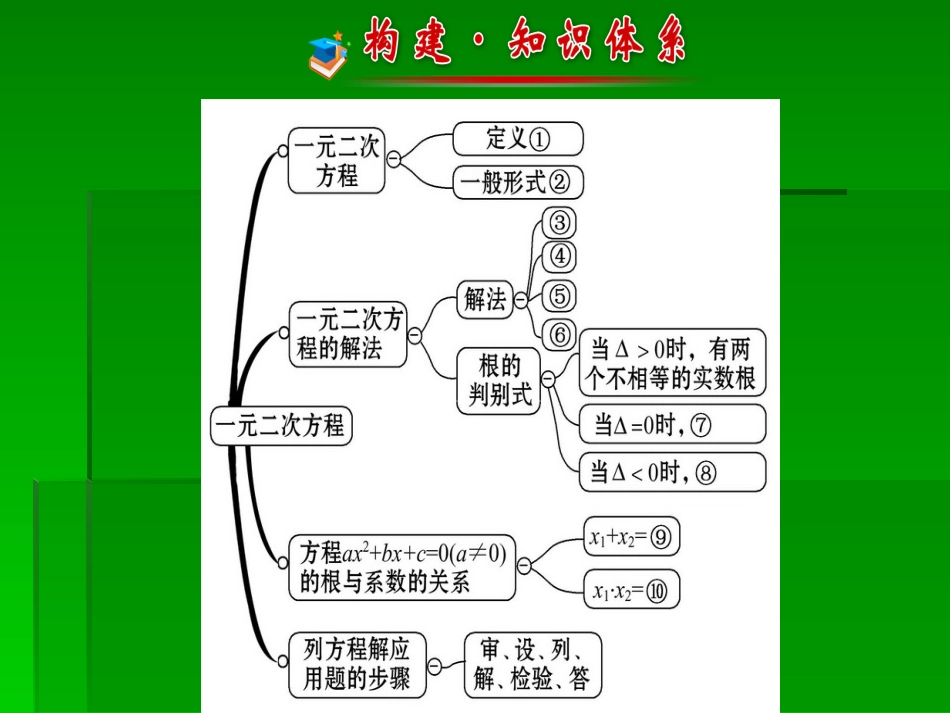
阶段专题复习第二十二章考点1一元二次方程的概念及解法1.一元二次方程必须同时满足以下三个条件.(1)整式方程.(2)只含有一个未知数.(3)未知数的最高次数为2.2.一元二次方程的四种解法.(1)直接开平方法.(2)因式分解法.(3)配方法.(4)公式法.3.一元二次方程解法选择.若没有特别说明,解法选择的基本顺序是直接开平方法→因式分解法→公式法.配方法使用较少,除非题目有明确要求才使用.1、(2012·安顺中考)已知1是关于x的一元二次方程(m-1)x2+x+1=0的一个根,则m的值是()(A)1(B)―1(C)0(D)无法确定2、已知关于x的方程(k+1)xk2+1+(k-3)x-1=0.(1)当k取何值时,它是一元一次方程.(2)当k取何值时,它是一元二次方程.3、(2012·荆门中考)用配方法解关于x的一元二次方程x2-2x-3=0,配方后的方程可以是()(A)(x-1)2=4(B)(x+1)2=4(C)(x-1)2=16(D)(x+1)2=16考点2根的判别式及根与系数的关系1.根的判别式的作用:不解方程判断方程有无实数根.2.根与系数的关系的作用:不解方程通过系数反映两根特征.3.一元二次方程的根的情况取决于Δ=b2-4ac的符号.(1)当Δ=b2-4ac>0时,方程有两个不相等的实数根.(2)当Δ=b2-4ac=0时,方程有两个相等的实数根.(3)当Δ=b2-4ac<0时,方程没有实数根.(4)对于以上三种情况,反之也成立.4.若x1,x2为方程ax2+bx+c=0(a≠0)的根,则x1+x2=x1·x2=ba,c.a1、(2012·通辽中考)已知方程x2-2x-1=0的两根分别是x1,x2,则=__________.1211xx2、(.(2012·广安中考)已知关于x的一元二次方程(a-1)x2-2x+1=0有两个不相等的实数根,则a的取值范围是()(A)a>2(B)a<2(C)a<2且a≠1(D)a<-23、已知关于x的方程x2-(m+2)x+(2m-1)=0.(1)求证:方程恒有两个不相等的实数根.(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长.考点3一元二次方程的应用【知识点睛】列一元二次方程解应用题的三点注意.(1)审题:准确找出已知量与未知量之间的关系.(2)设元:分为直接设未知数和间接设未知数两种,对于直接设未知数列方程比较困难或列出的方程比较复杂时,要考虑采用间接设未知数.(3)检验:求出方程的解后,必须检验所求的解是否符合题目要求或客观实际,不符合的解需要舍去.1、(2012·保山中考)据调查,某市2011年的房价为4000元/m2,预计2013年将达到4840元/m2,求这两年的年平均增长率,设年平均增长率为x,根据题意,所列方程为()(A)4000(1+x)=4840(B)4000(1+x)2=4840(C)4000(1-x)=4840(D)4000(1-x)2=48402、(2012·白银中考)某玩具店购进一种儿童玩具,计划每个售价36元,能盈利80%.在销售中出现了滞销,于是先后两次降价,售价降为25元.(1)求这种玩具的进价.(2)求平均每次降价的百分率.(精确到0.1%)