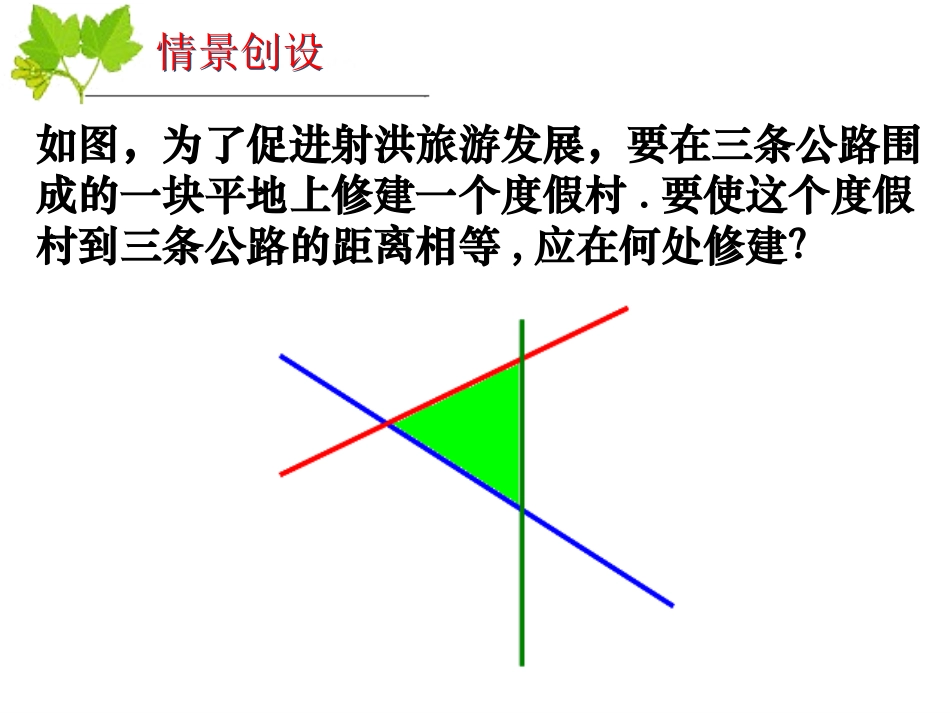
课题课题§13.5§13.5课题课题§13.5§13.5教师:王建军细心观察积极探索在观察中发现特点在探索中提高能力让我们一起走进有趣有用的数学世界如图,为了促进射洪旅游发展,要在三条公路围成的一块平地上修建一个度假村.要使这个度假村到三条公路的距离相等,应在何处修建?情景创设情景创设复习提问1、角平分线的概念一条射线一条射线把一个角把一个角分成两个相等的角分成两个相等的角,,这条射线叫做这个角的平分线。这条射线叫做这个角的平分线。oBMA122、点到直线距离:从直线外一点到这条直线的垂线段叫做点到直线的距离。2、点到直线距离:从直线外一点到这条直线的垂线段叫做点到直线的距离。PABO线段的长度3.互逆命题:两个命题,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论是第二个命题的条件。那么这两个命题叫做互逆命题。3.互逆命题:两个命题,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论是第二个命题的条件。那么这两个命题叫做互逆命题。动动手将你手中的∠AOB对折,使角的两条边OA与OB重合.请问折痕射线OM有何特点?∠AOB是轴对称图形吗?ABOM结论:角是轴对称图形.对称轴是角平分线所在的直线在角平分线OM上任取一点P,过P点分别作OA和OB的垂线段PC和PD,画一画,量一量,折一折,观察PC和PD有什么数量关系?再取一点,按上述同样的方法试验又如何?请你大胆猜想你能得出什么结论?角的平分线有什么性质?角平分线上的点到这个角的两边的距离相等.观察后大胆猜想已知:如图,OC是∠AOB的平分线,点P在OC上,PDOA⊥,PEOB⊥,垂足分别是D,E。求证:PD=PE证明: PDOA⊥,PEOB⊥(已知)∴∠PDO=PEO=90∠(垂直的定义)在△PDO和△PEO中∴PD=PE(全等三角形的对应边相等)∠PDO=PEO∠∠AOC=BOC∠OP=OP∴△PDO△PEO△(AAS)角的平分线上的点到这个角的两边的距离相等。DPEAOBC验证结论又 OC是∠AOB的平分线∴∠AOC=BOC∠角平分线的性质定理:角的平分线上的点到角两边的距离相等用符号语言表示为:AOBPED12 ∠1=∠2PD⊥OA,PE⊥OB∴PD=PE(角的平分线上的点到角的两边的距离相等)推理的理由有三个,必须写完全,不能少了任何一个。它是证明两条线段相等的又一方法 如图,AD平分∠BAC(已知)∴=,()角的平分线上的点到这个角的两边的距离相等。ADCBBDCD(×)学以致用学以致用(抢答:看谁反应最快) 如图,DCAC⊥,DBAB⊥(已知)∴=,()角的平分线上的点到这个角的两边的距离相等。ADCBBDCD(×) AD平分∠BAC,DCAC⊥,DBAB⊥(已知)∴=,()DBDC角的平分线上的点到这个角的两边的距离相等。ADCB√不必再证全等已知△ABC中,C=90∠0,AD平分∠CAB,且BC=8,BD=5,求点D到AB的距离是多少?ABCDE你会吗?加深印象(看谁学得最好)加深印象(看谁学得最好)角平分线性质定理:角的平分线上的点到这个角的两边的距离相等。条件结论性质定理逆命题如果一个点在角的平分线上那么这个点到角两边的距离相等如果角内部的一个点到角两边的距离相等那么这个点在角平分线上角平分线性质定理的逆命题及论证:角的内部到角两边的距离相等的点,在这个角的平分线上。已知:如图,QDOA⊥,QEOB⊥,垂足分别是D,E,QD=QE.求证:点Q在∠AOB的平分线上ODABEQ分析:为了证明点Q在∠AOB的平分线上,可以作射线OQ,然后转化证明∠EOQ=∠DOQ,则只需证明Rt△QDO≌Rt△QEO,就行了.老师期望:请认真学习P97规范的证明过程.老师期望:请认真学习P97规范的证明过程.几何语言: Q是∠AOB内的一点,QD⊥OA于D,QE⊥OB于E且QD=QE∴OQ是∠AOB的平分线(到角两边距离相等的点在这个角的平分线上)几何语言: Q是∠AOB内的一点,QD⊥OA于D,QE⊥OB于E且QD=QE∴OQ是∠AOB的平分线(到角两边距离相等的点在这个角的平分线上)角平分线性质定理的逆定理:角的内部到角两边的距离相等的点,在这个角的平分线上。角平分线性质定理的逆定理:角的内部到角两边的距离相等的点,在这个角的平分线上。lABC1、如图,在直线上找一点P,使P到射线AB和AC的距离相等P作法:作∠BAC的平分线,交直线l于点P。则点P为所求作的点。应用与提高(P98练习题)(看谁学得最好)l例已知:如下图,△ABC的角...