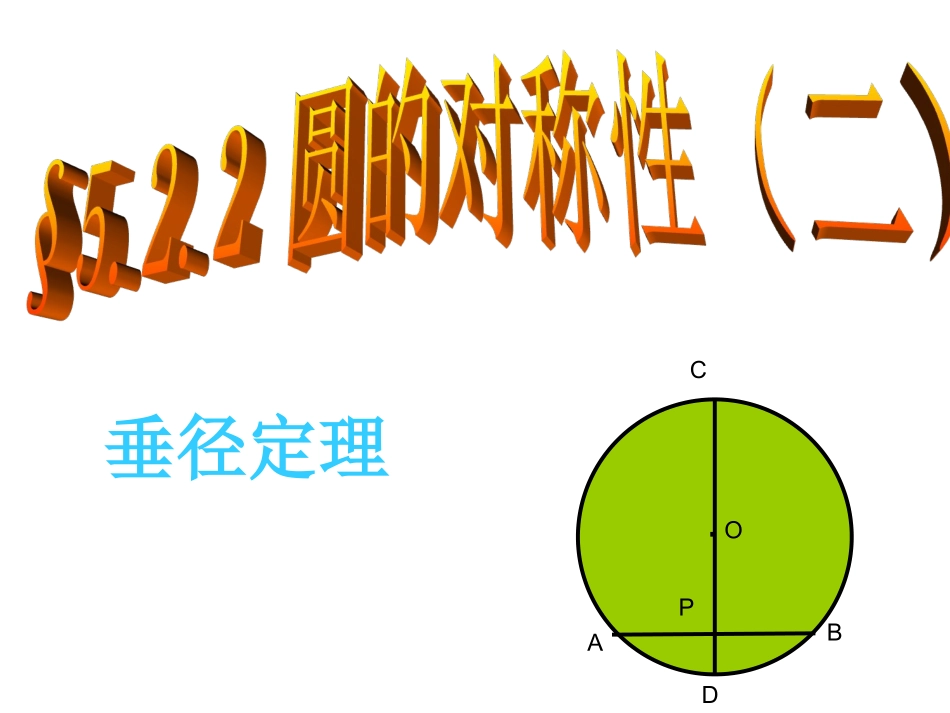
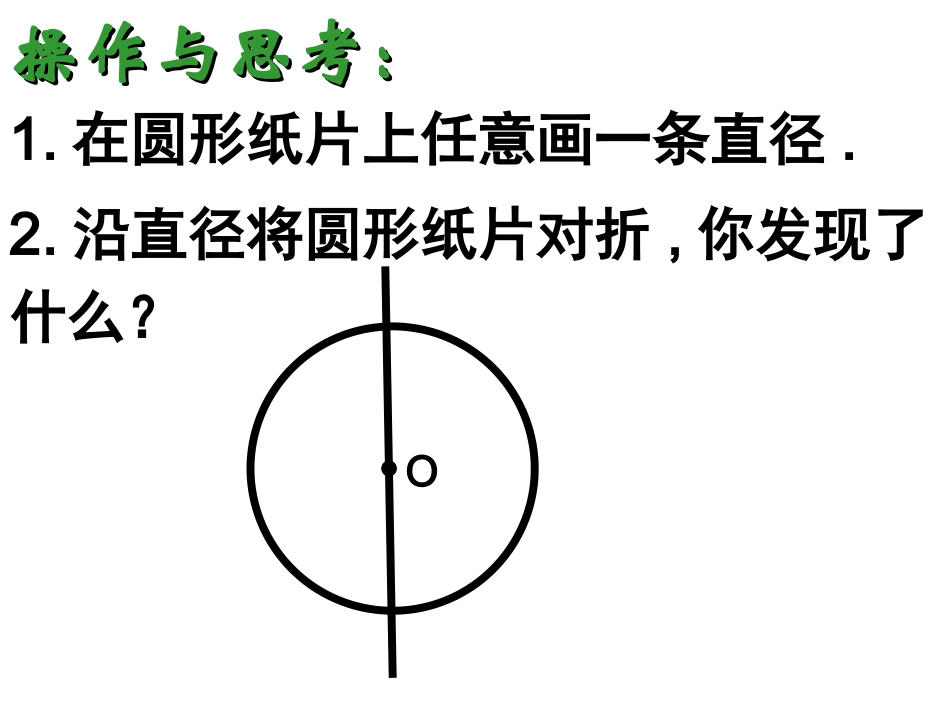
垂径定理BPOACD·1.圆是中心对称图形,圆心是它的对称中心。2.在同圆或等圆中,如果两个圆心角,两条弧,两条弦中有一组量相等,那么它们所对应的其余各组都分别相等。Ô²ÐĽǵĶÈÊýÓëËüËù¶ÔµÄ»¡µÄ¶ÈÊýÏàµÈ¡£3.复习复习O操作与思考:操作与思考:1.在圆形纸片上任意画一条直径.2.沿直径将圆形纸片对折,你发现了什么?圆的对称性圆是轴对称图形吗?想一想它的对称轴是什么?你能找到多少条对称轴?●OACBNMD任意一条直径都是圆的对称轴.O圆是轴对称图形,过圆心的每一条直线都是它的对称轴.判断如果AB是⊙O的弦,画直径CD⊥AB于P,将纸片沿着CD对折,通过折叠活动,你发现了什么?OBAPDC发现:PA=PB︵︵AD=BDAC=CB︵︵如果AB是⊙O的弦,画直径CD⊥AB于P,将纸片沿着CD对折,通过折叠活动,你发现了什么?OBAPDC发现:PA=PB︵︵AD=BDAC=CB︵︵连接OA,OB,则OA=OB.在△OAB中, OA=OB,CD⊥AB∴AP=BP.∴点A和点B关于CD对称. ⊙O关于直径CD对称,∴当圆沿着直径CD对折时,点A与点B重合,⌒⌒AC和BC重合,⌒⌒AD和BD重合.⌒⌒∴AC=BC,⌒⌒AD=BD.证明:DCBAOP垂径定理垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.(1)过圆心(3)平分弦MODBA(2)垂直于弦(5)平分弦所对的劣弧(4)平分弦所对的优弧③AM=BM,①CD是直径②CDAB⊥⌒⌒④AC=BC,⌒⌒⑤AD=BD.MODCBAODAB⊥于M结论:BPOACD· 在⊙O中,CD是直径,CDΑΒP,于AD=BD,AC=BC∴AP=BP,几何语言:垂径定理垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.PODCBAPODCBAPODCBAPODBA练1:1.下列图形能用垂径定理的是___ABCODE2.如图,AB是⊙O的直径,CD为弦,CDAB⊥于E,则下列结论中不一定成立的是()A.COE=DOEB.CE=DE∠∠C.OE=BED.BD=BC∟3.如图,M为⊙O内一点,(1)作一条弦AB,使AB过点M且AM=BM.(2)你能画过点M最长的弦吗?OM∟AB最短4.过⊙O内一点M的最长弦长为10cm,最短弦长为8cm,那么OM长为____.OM∟AB5.如图,O⊙的直径为10,弦AB长为8,P是弦AB上的动点,则OP的长的取值范围是____.ABOM如图,⊙O的直径是10,弦AB的长为8,P是AB上的一个动点,①则OP的求值范围是。②使线段OP的长度为整数值的P点位置有个。OBAp1p2PC注意圆的轴对称性3≤OP≤55例1.已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点,AC与BD相等吗?为什么?P.ACDBO练2:如图,OA=OB,AB交⊙O与点C、D,AC与BD是否相等?为什么?例2.如图,在⊙O中,AB=8cm,圆心O到AB的距离为3cm,求⊙O的半径.EABO弦的一半半径弦心距弦的一半2+弦心距2=半径2∟要求弦要求弦,,只需求弦的一半只需求弦的一半,,常作常作垂直于弦的垂直于弦的半径半径,,构成构成直角直角三角形三角形..例.如图,已知在圆O中,弦AB的长为8㎝,圆心O到AB的距离为3㎝,求圆O的半径。变式1:在半径为5㎝的圆O中,有长8㎝的弦AB,求点O与AB的距离。E变式2:在半径为5㎝的圆O中,圆心O到弦AB的距离为3㎝,求AB的长。OAB例3.如图,圆O的弦AB=8㎝,DC=2㎝,直径CEAB⊥于D,求半径OC的长。DCEOAB例4.在圆O中,直径CEAB⊥于D,OD=4㎝,弦AC=㎝,求圆O的半径。10DCEOAB例5.某居民区一处圆形下水管道破裂,修理人员准备更换一段新管道.如图所示,污水水面宽度为60cm,水面至管道顶部距离为10cm,问修理人员应准备半径多大的管道?10cm60cmABOOBAEF解:过O点作OE⊥AB,并延长OE交⊙O于F,连接OA222)10(30RR垂径定理和勾股定理相结合,构造直角三角形,把圆的问题化归为直线形问题解决。10cm60cmABO思考:在例2中,我们已计算出⊙O的半径R=50cm,如果水面宽度由60cm变为80cm,那么污水面下降了多少cm?10cm60cmABOCD两弦在圆心同旁两弦在圆心两旁DCO·BAFEO·BADCFER=50cm;CD=80cmCD作垂径,连半径,构造直角三角形注意圆的对称性1.在半径为50的⊙O中,弦AB=50,计算:⑴点O与AB的距离;AOB∠的度数.OBAP∟练3:2.在直径为650mm的圆柱形油槽内装入一些油后,截面如图,若油面宽AB=600mm,求油的最大深度。ф650mmAB600mmOABDC∟3.1300年前,我国隋朝建造的赵州石拱桥的桥拱是圆弧形,它的跨度(弧所对的弦的长)为37.4米,拱高(弧的中点到弦的距离,也叫弓形高)为7....