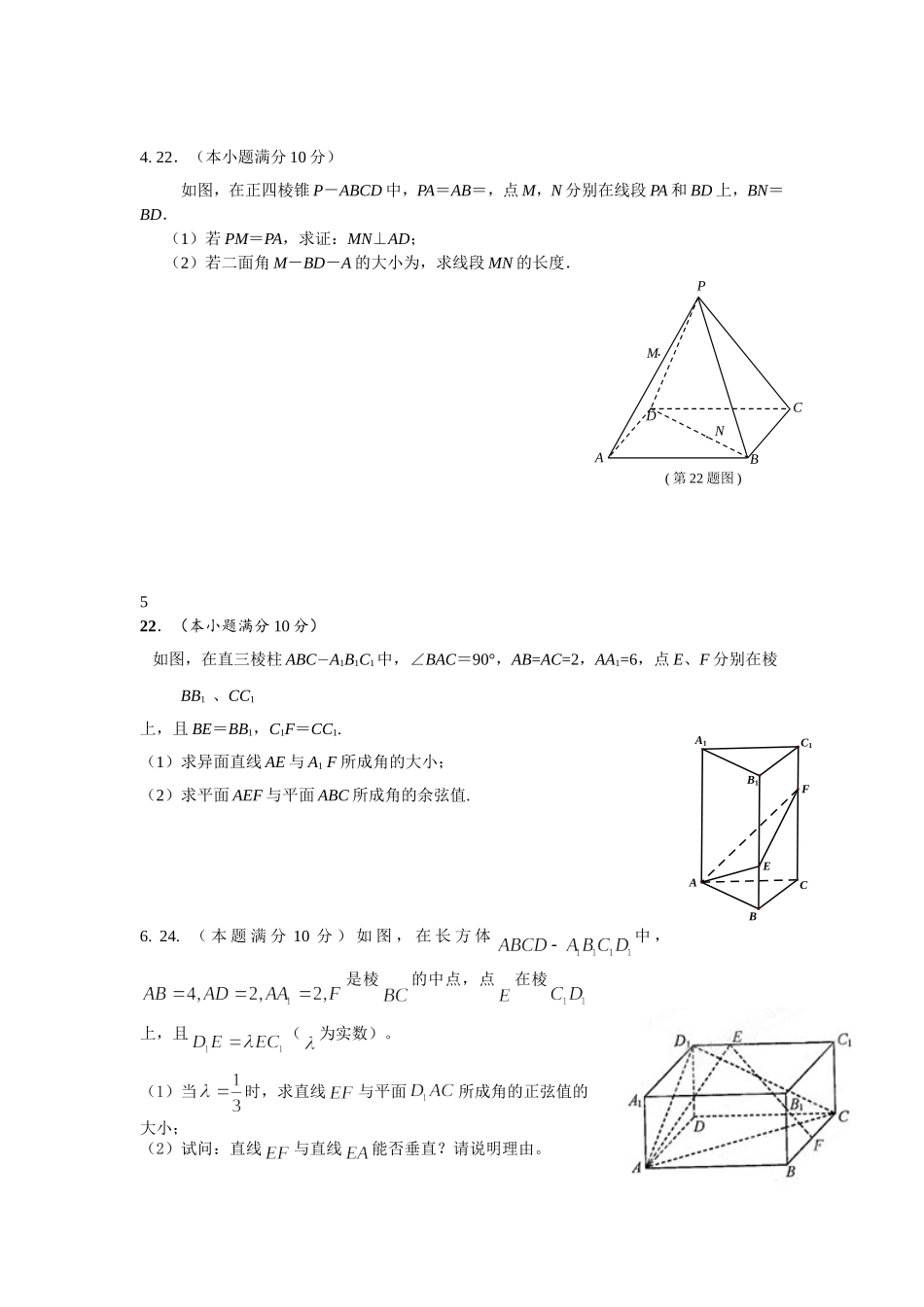
1.如图,是直角梯形,∠=90°,∥,=1,=2,又=1,∠=120°,⊥,直线与直线所成的角为60°.(Ⅰ)求二面角的的余弦值;(Ⅱ)求点到面的距离.2.在长方体ABCD—A1B1C1D1中,,点E是棱AB上一点.且.(1)证明:;(2)若二面角D1—EC—B的大小为,求的值.3.23、已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,底面ABCD,且PA=AD=DC=AB=1,M是PB的中点.(1)证明:面PAD⊥面PCD;(2)求AC与PB所成的角的余弦值;(3)求二面角A-MC-B所成的余弦值。ABCDD1A1B1C1E(第22题)4.22.(本小题满分10分)如图,在正四棱锥P-ABCD中,PA=AB=,点M,N分别在线段PA和BD上,BN=BD.(1)若PM=PA,求证:MN⊥AD;(2)若二面角M-BD-A的大小为,求线段MN的长度.522.(本小题满分10分)如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,AA1=6,点E、F分别在棱BB1、CC1上,且BE=BB1,C1F=CC1.(1)求异面直线AE与A1F所成角的大小;(2)求平面AEF与平面ABC所成角的余弦值.6.24.(本题满分10分)如图,在长方体中,是棱的中点,点在棱上,且(为实数)。(1)当时,求直线与平面所成角的正弦值的大小;(2)试问:直线与直线能否垂直?请说明理由。C··PMABDN(第22题图)CAA1C1B1BEFA1BADCBAO(第22题)EBAB1CBAA1CBACBAC1D171.如图,直三棱柱ABC-A1B1C1中,底面是等腰直角三角形,AB=BC=,BB1=3,D为A1C1的中点,F在线段AA1上.(1)AF为何值时,CF⊥平面B1DF?(2)设AF=1,求平面B1CF与平面ABC所成的锐二面角的余弦值.[来源:Zxxk.Com]22.在正方体1111ABCDABCD中,O是AC的中点,E是线段D1O上一点,且D1E=λEO.(1)若λ=1,求异面直线DE与CD1所成角的余弦值;(2)若平面CDE⊥平面CD1O,求λ的值.1.(Ⅰ) ∴.在平面内,过作,建立空间直角坐标系(如图)由题意有,设,则ABCC1B1A1FD由直线与直线所成的解为,得,即,解得∴,设平面的一个法向量为,则,取,得,平面的法向量取为设与所成的角为,则.显然,二面角的平面角为锐角,故二面角的余弦值为.………………5分(Ⅱ),,,,.设平面的一个法向量,则,取,得,则点到平面的距离.2.3.23、解:因为PA⊥PD,PA⊥AB,AD⊥AB,以A为坐标原点AD长为单位长度,如图建立空间直角坐标系,则各点坐标为A(0,0,0)B(0,2,0),C(1,1,0),D(1,0,0),P(0,0,1),M(0,1,.(Ⅰ)证明:因由题设知AD⊥DC,且AP与AD是平面PAD内的两条相交直线,由此得DC⊥面PAD.又DC在面PCD上,故面PAD⊥面PCD.(Ⅱ)解:因(Ⅲ)解:在MC上取一点N(x,y,z),则存在使要使为所求二面角的平面角.4.22.(本小题满分10分)证明:连接AC,BD交于点O,以OA为x轴正方向,以OB为y轴正方向,OP为z轴建立空间直角坐标系.因为PA=AB=,则A(1,0,0),B(0,1,0),D(0,-1,0),P(0,0,1).(1)由BN=BD,得N(0,,0),由PM=PA,得M(,0,),所以MN=(-,,-),AD=(-1,-1,0).因为MN·AD=0.所以MN⊥AD.………………………………………4分(2)因为M在PA上,可设PM=λPA,得M(λ,0,1-λ).所以BM=(λ,-1,1-λ),BD=(0,-2,0).设平面MBD的法向量n=(x,y,z),由得其中一组解为x=λ-1,y=0,z=λ,所以可取n=(λ-1,0,λ).………………………………8分因为平面ABD的法向量为OP=(0,0,1),所以cos=||,即=,解得λ=,从而M(,0,),N(0,,0),所以MN==.………………………………………10分5.解:(1)建立如图所示的直角坐标系,则,,,,从而,.………………2分记与的夹角为,则有.由异面直线与所成角的范围为,得异面直线与所成角为60º.……4分(2)记平面和平面的法向量分别为n和m,则由题设可令,且有平面的法向量为,,.由,得;由,得.所以,即.………………8分记平面与平面所成的角为,有.由题意可知为锐角,所以.………………10分6.24.由解得取,则,因为,,,所以因为,所以是锐角,是直线与平面所成角的余角,所以直线与平面所成角的正弦值为.⑵假设,则,因为,,所以,化简,得,因为,所以该方程无解,所以假设不成立,即直线不可能与直线垂直.7.3、解:(1)因为直三棱...