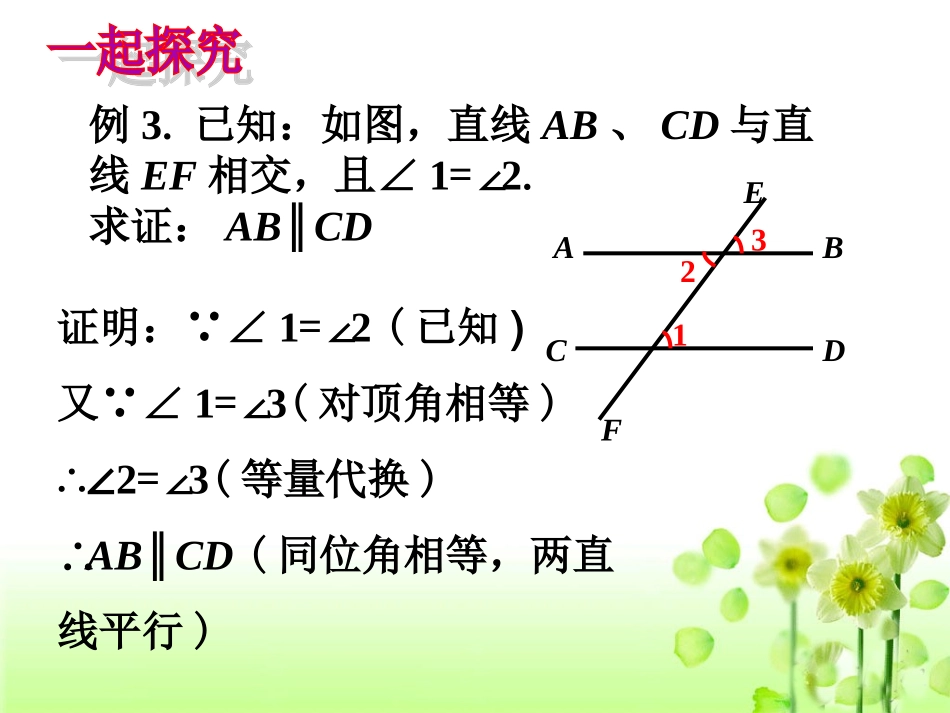
平行线的性质定理一两条平行线被第三条直线所截,内错角相等.1.指出定理的条件和结论,并画出图形,结合图形写出已知、求证.2.说说你的证明思路,试着写出证明过程.例3.已知:如图,直线AB、CD与直线EF相交,且∠1=∠2.求证:AB∥CDFABDCE321证明:∵∠1=∠2(已知)又∵∠1=∠3(对顶角相等)∴∠2=∠3(等量代换)∴AB∥CD(同位角相等,两直线平行)已知:如图,直线ABCD∥,AB,CD被直线EF所截,∠1和∠2是同旁内角.求证:∠1+∠2=180°.ABDCE321例4.已知:如图,∠AOB=∠BOC=180°,OE平分∠AOB,OF平分∠BOC求证:OE⊥OF∵OE平分∠AOB,OF平分∠BOC,(已知)∴∠1=∠AOB,∠2=∠BOC.(角平分线的定义)又∵∠AOB=∠BOC=180°,(已知)∴∠1+∠2=(∠AOB+∠BOC)=90°.(等式性质)∴OE⊥OF(垂直的定义)补充完成下列各题的证明,并填上推理的依据.1.已知:如图,AB∥CD,AD∥BC.求证:∠A=∠C.证明:∵AB∥CD,()∴∠A+∠D=180°.()∵AD∥BC,()∴∠C+∠D=180°.()∴∠A+∠D=∠C+∠D()∴∠A=∠C.()已知条件两直线平行,同旁内角相等.已知条件两直线平行,同旁内角互补.角的性质与相同角互补的角相等2.已知:如图,DC∥AB,DF平分∠CDB,BE平分∠ABD.求证:∠1=2.∠证明:∵DC∥AB,()∴∠ABD=∠CDB()∵DF平分∠CDB,BE平分∠ABD.()∴∠1=∠CDB,()∴∠2=∠ABD.()∴∠1=2.()∠两直线平行,内错角角相等.已知条件角平分线性质.21已知条件21角平分线性质.角的性质