四边形复习开课201541--VIP免费

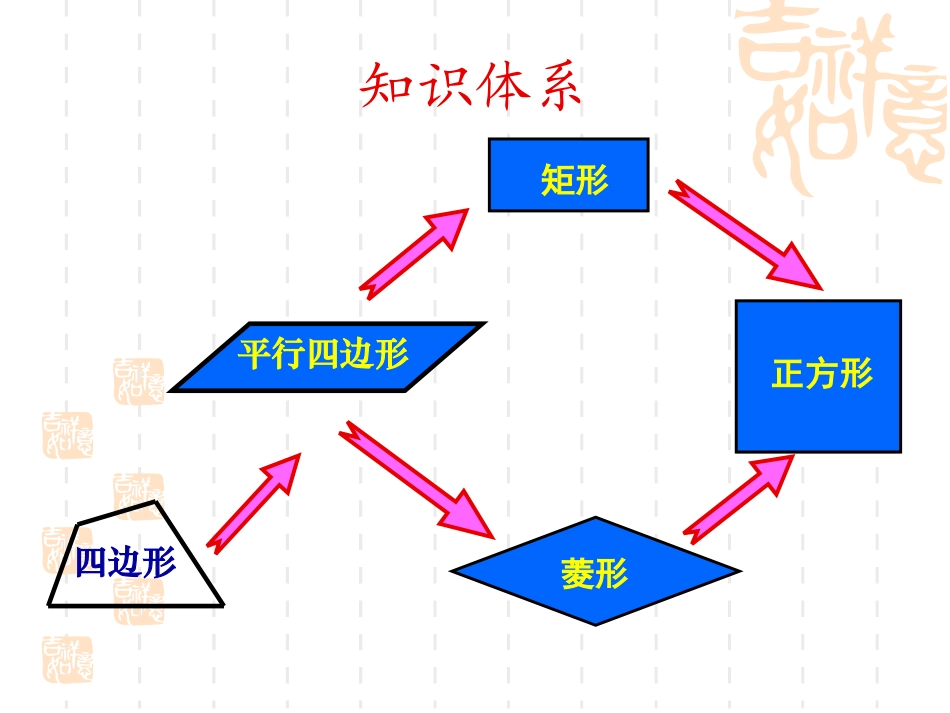
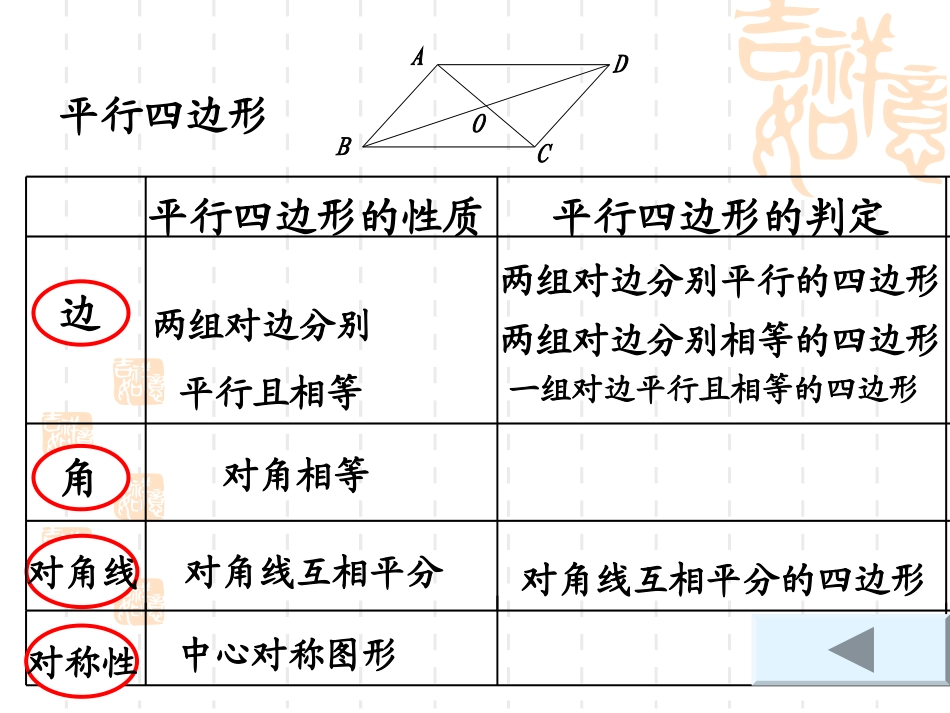
四边形复习课四边形复习课初三数学备课组知识体系四边形矩形平行四边形菱形正方形平行四边形的性质平行四边形的判定边角对角线两组对边分别平行且相等对角相等对角线互相平分BDACO两组对边分别平行的四边形一组对边平行且相等的四边形两组对边分别相等的四边形对角线互相平分的四边形对称性中心对称图形平行四边形性质判定矩形ACBDO性质判定对称性角对角线矩形ACBDO性质判定对称性轴对称角矩形的四个角都是直角对角线矩形的两条对角线相等矩形ACBDO性质判定对称性轴对称角矩形的四个角都是直角①有一个角是直角的平行四边形是矩形②有三个角是直角的四边形是矩形对角线矩形的两条对角线相等③对角线相等的平行四边形是矩形矩形ACBDO性质判定对称性边对角线2.性质：菱形ABCDO性质判定对称性轴对称边菱形的四条边都相等对角线菱形的两条对角线互相垂直,并且每条对角线平分一组对角2.性质：菱形ABCDO性质判定对称性轴对称边菱形的四条边都相等①一组邻边相等的平行四边形,②四条边都相等的四边形是菱形.对角线菱形的两条对角线互相垂直,并且每条对角线平分一组对角③对角线互相垂直的平行四边形是菱形2.性质：菱形ABCDO性质判定对称性具有矩形菱形所有性质边角对角线2.性质：正方形性质判定对称性具有矩形菱形所有性质有一个角是直角，且有一组邻边相等的平行四边形是正方形边有一组邻边相等的矩形是正方形.角有一个角是直角的菱形是正方形.对角线2.性质：正方形1、平行四边形ABCD中，AE,AF为BC,CD边上的高，(1)若∠BAE=40度，则∠D=____,∠EAF=_____.(2)若平行四边形ABCD的周长为40，AE=6，AF=9,则AB=_____,▱ABCD的面积=______.练一练：50O50O8722、如图，平行四边形ABCD的周长为40cm，AB≠AD，AC、BD相交于点O，EOBD⊥交AD于点E(1)△ABE的周长为_____cm(2)若点P为直线OE上的一个动点，△ABP周长的最小值为_____cmP20203、已知四边形ABCD的对角线AC、BD相交于点O,有下列四个条件：①OB=ODAD②∥BCAB=CD∠BAD=∠BCD∠∠.从中任选两个条件，能够说明它是平行四边形的选法有_______种.oDBCA悟一悟：24、已知平行四边形ABCD的对角线AC、BD相交于点O,有下列五个条件：①OB=OAAD=DCBD②③平分∠ABCBAD=ADC④∠∠⑤AOB=BOC∠∠.从中任选两个条件，能够说明它是正方形的选法有____种.oDBCA6ACBDOABCDO5、（2013·白银)如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于点F，且AF＝BD，连接BF.(1)四边形AFBD是____________形.(2)当△ABC满足____________时，四边形AFBD是矩形(3)当△ABC满足____________时，四边形AFBD是菱形(4)当△ABC满足________________________时，四边形AFBD是正方形做一做：AB=AC且6、（2010•宁夏）在△ABC中，∠BAC=45°，ADBC⊥于D，将△ABD沿AB所在的直线折叠，使点D落在点E处；将△ACD沿AC所在的直线折叠，使点D落在点F处，分别延长EB、FC使其交于点M．（1）判断四边形AEMF的形状，并给予证明；（2）若BD=1，CD=2，试求四边形AEMF的面积．试一试：7、如图，在平面直角坐标系中，已知矩形ABCD的三个顶点B（1，0），C（3，0），D（3，4）．以A为顶点的抛物线y=ax2+bx+c过点C．动点P从点A出发，沿线段AB向点B运动．同时动点Q从点C出发，沿线段CD向点D运动．点P，Q的运动速度均为每秒1个单位．运动时间为t秒．过点P作PEAB⊥交AC于点E．（1）直接写出点A的坐标，并求出抛物线的解析式；（2）过点E作EFAD⊥于F，交抛物线于点G，当t为何值时，△ACG的面积最大？最大值为多少？（3）在动点P，Q运动的过程中，平面内是否存在点H，使以C，Q，E，H为顶点的四边形为菱形？若存在，请直接写出t的值；若不存在，清说明理由。小结：这节课我们学到了什么？谢谢指导！谢谢指导！初三数学备课组