平面与平面垂直的性质(例题练习针对性)VIP免费

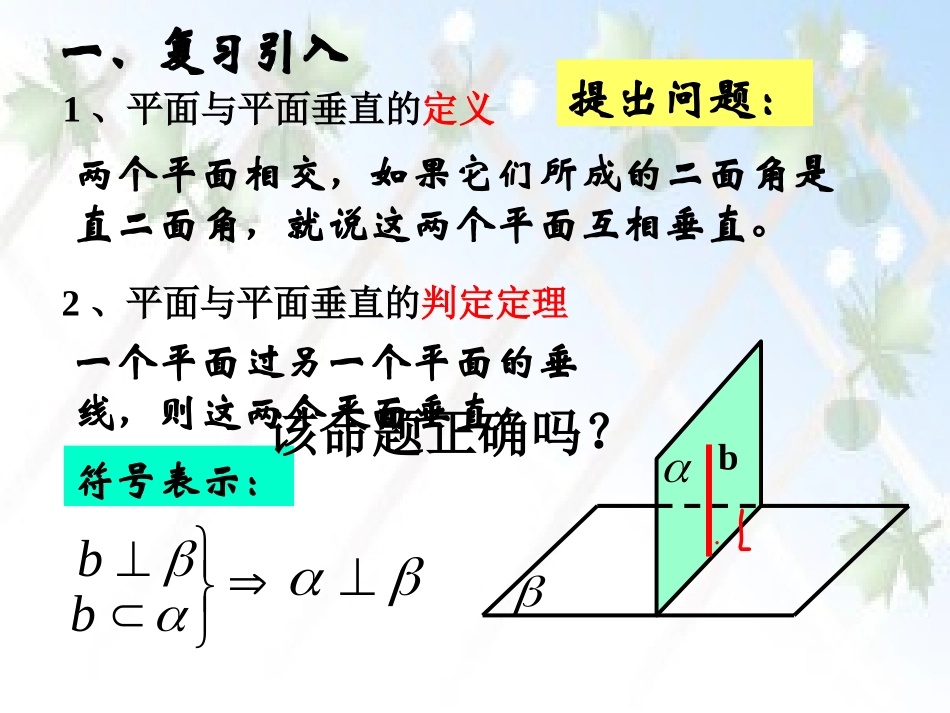
1、平面与平面垂直的定义2、平面与平面垂直的判定定理一个平面过另一个平面的垂线，则这两个平面垂直。符号表示：b两个平面相交，如果它们所成的二面角是直二面角，就说这两个平面互相垂直。bb提出问题：该命题正确吗？bⅠ.观察实验观察两垂直平面中,一个平面内的直线与另一个平面的有哪些位置关系?Ⅱ.概括结论lllb平面与平面垂直的性质定理bb两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.bb该命题正确吗？符号表示：bⅡ.概括结论llbblbAOaB设直线b即AO交直线l于O，在平面内过O作直线OBl；blAOB即为与所成的二面角的平面角。90AOBbOBblb又即而分析：lbllbbb两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.简述为：面面垂直线面垂直符号表示：平面与平面垂直的性质定理例,四棱锥P-ABCD的底面是矩形AB=2，，侧面PAB是等边三角形，且侧面PAB⊥底面ABCD.求证：侧面PAB⊥侧面PBC；2BCPABCDE练：已知SA⊥平面ABC，平面SAB⊥平面SBC，求证：AB⊥BCSABCD如图，边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面，BC=，M为BC的中点。证明：AMPM⊥。PABCDM22练：已知SA⊥平面ABC，平面SAB⊥平面SBC，求证：AB⊥BCSABCD证明：过点A作ADSB⊥于D，∵平面SAB⊥平面SBC，平面SAB∩平面SBC=SB，∴AD⊥平面SBC∵SA⊥平面ABC，BC平面ABC∴SABC⊥∵SA∩AD=A，∴BC⊥平面SAB∵AB平面ABC∴ABBC⊥∵BC平面SBC∴AD⊥BC“从已知想性质，从求证想判定”这是证明几何问题的基本思维方法．如图，边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面，BC=，M为BC的中点。（1）证明：AMPM⊥（2）求二面角P-AM-D的大小(3)求点D到平面AMP的距离。PABCDM22