探索三角形相似的条件(1)戴琴VIP免费

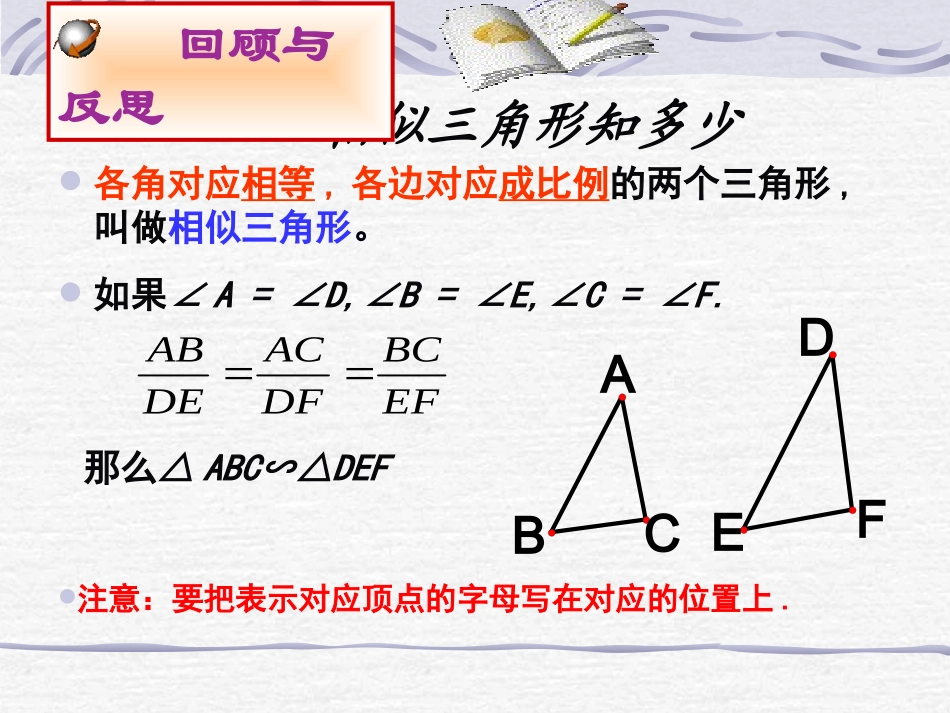
1.初步掌握两个三角形相似的判定条件。2.经历两个三角形相似条件的探索过程,进一步发展学生的探索、交流能力，以及动口、动手、动脑自觉获取知识的习惯。3.运用三角形相似条件解决简单的实际问题.学习目标相似三角形知多少各角对应相等,各边对应成比例的两个三角形,叫做相似三角形。如果∠A=∠D,∠B=∠E,∠C=∠F.EFBCDFACDEAB注意：要把表示对应顶点的字母写在对应的位置上.那么△ABC∽△DEF回顾与反思ABCDEF如图，小明用一张纸遮住了3个三角形的一部分，你能画出这3个三角形吗？ABA′A′′B′B′′操作探索ABA′A″B′B″（1）如图，如果∠A＝∠A′，∠B＝∠B′，AB＝A′B′，那么第一个三角形与第二个三角形全等吗？为什么？CC′C″操作探索（2）如图，如果∠A＝∠A″，∠B＝∠B″，2AB＝A″B″，那么第一个三角形与第三个三角形相似吗？请与同学交流。ABA′A″B′B″操作探索C″C′C友情提示:①∠C=∠C″吗？②量一量，算一算、比一比，对应边的比值是否相等？③这两个三角形相似吗？（3）如图，如果∠A＝∠A″，∠B＝∠B″操作探索设A″B″＝kAB,改变k值的大小，再试一试ABCDEF如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似。如图，在△ABC和△DEF中∵∠A=∠D,∠B=∠E，∴△ABCDEF∽△两角对应相等的两个三角形相似.交流讨论例题欣赏ABCA′B′C′1、如图，在△ABC和△A′B′C′中，∠A＝50°，∠B＝∠B′＝60°，∠C′＝70°，△ABC与△A′B′C′相似吗？为什么？解：△ABC∽△A′B′C′在△ABC中∵∠A＝50°，∠B＝60°∴∠C＝180°-（50°+60°）=70°在△ABC和△A′B′C′中∵∠B＝∠B′，∠C＝∠C′∴△ABC∽△A′B′C′(1)49(2)7138(3)41(4)4938(5)7171找一找，下面图形中有几对相似三角形？小试牛刀例题欣赏ABCDE2、如图，DE∥BC，分别交AB、AC于点D、E，△ADE与△ABC相似吗？为什么？解：△ADEABC∽△在△ADE和△ABC中，∵DEBC∥∴∠ADE＝∠B，∠AED＝∠C∴△ADEABC∽△ABCED变式变式：如图，如果：如图，如果DE∥BCDE∥BC，那么，那么△△ADEADE与与△△ABABCC相似吗？为什么？相似吗？为什么？例题欣赏解：△ADE∽△ABC在△ADE和△ABC中，∵DE∥BC∴∠D＝∠B，∠E＝∠C∴△ADE∽△ABCABCDEABCED几何语言：∵DE∥BC∴△ADE∽△ABC平行于三角形一边的直线与其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似。交流讨论生活中的数学如图,在测量小玻璃管管径的量具上,AB长为5mm,AC被分为50等份.如果玻璃管的管径DE正好对着量具上30等份处(DE∥AB).那么管径的长等于3mm.为什么?如果DE正好对着量具上35等份处呢?∴∴∴DE=3mmABDEACCD55030DE解：∵DEAB∥∴△CDECAB∽△DE正好对着量具上35等份处时DE=3.5mmADCBGFE如图，平行四边形ABCD中，F是AD延长线上一点，连接BF，交AC于G，交CD于E，那么图中相似三角形共有＿＿＿对思维训练抓平行线,找基本图形,确定相似三角形.我有哪些收获呢？我有哪些收获呢？还有什么疑问?学而不思则罔回头一看，我想说…过△ABC(∠C>∠B)的边AB上一点D作一条直线与另一边ＡＣ相交，截得的小三角形与△ABC相似，这样的直线最多有几条？请把它们一一作出来。这样的直线有几条？CD●ＡＢ发散探究BCADEEBCAD△△ADE∽△ABCADE∽△ABC△△AED∽△ABCAED∽△ABC∠∠A=A∠A=A∠∠∠ADE=B∠ADE=B∠∠∠A=A∠A=A∠∠∠ADE=C∠ADE=C∠作作DE,DE,使∠使∠ADE=∠BADE=∠B作作DE,DE,使∠使∠ADE=∠CADE=∠C答：这样的直线有两条,如下图∴∴∵∵发散探究过△ABC(∠C>∠B)的边AB上一点D作一条直线与另一边相交，截得的小三角形与△ABC相似，这样的直线最多有几条？请把它们一一作出来。若把条件“与另一边ＡＣ相交”改为“与另一边相交”，这样的直线最多又有几条？CD●ＡＢ发散探究作业：《教材》P95-961、2、3、4