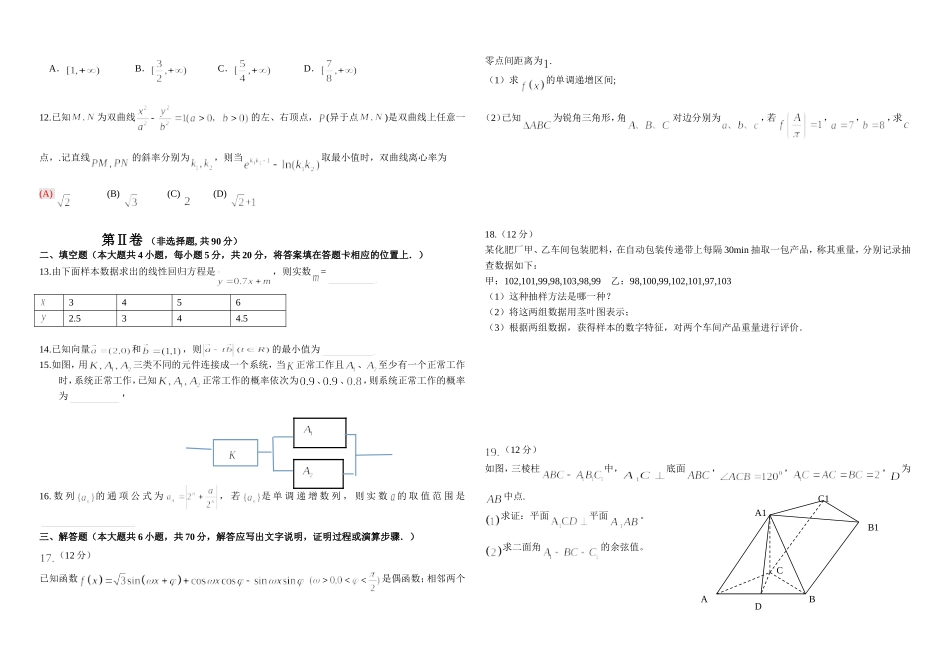
哈师大附中2015年第三次模拟考试数学试卷(理工类)第I卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.)设集合,,则复数,则的共轭复数的虚部是()A.B.C.D.3.已知一组数据的平均数是,方差是,那么另一组数据的平均数和方差分别是()A.B.C.D.4.已知,则角所在的象限是第一象限第二象限第三象限第四象限5.过原点的直线与圆有公共点,则直线倾斜角的取值范围为()A.B.C.D.6.等比数列中,,则:()A.B.C.D..7.有三个命题,其中真命题的个数是()(1)“两条直线无公共点”是“这两条直线为异面直线”的必要而不充分条件;(2)“一条直线垂直于一个平面内无数条直线”是“这条直线垂直于这个平面”的充要条件;(3)是平面外的两条直线,且∥,则“”是“”的充分而不必要条件.A.3B.2C.1D.08.如图,网格纸上小正方形的边长为1,图中粗线画出的是一个几何体的三视图,则该几何体的表面积是(A)(B)(B)(C)(D)9.阅读如图所示的程序框图,则该算法的功能是A.计算数列的前项和B.计算数列的前项和C.计算数列的前项和D.计算数列的前项和10..已知函数,则()A.B.C.D.11.已知函数,若时,恒成立,则函数的取值范围为()A.B.C.D.12.已知为双曲线的左、右顶点,(异于点)是双曲线上任意一点,.记直线的斜率分别为,则当取最小值时,双曲线离心率为(A)(B)(C)(D)第Ⅱ卷(非选择题,共90分)二、填空题(本大题共4小题,每小题5分,共20分,将答案填在答题卡相应的位置上.)13.由下面样本数据求出的线性回归方程是,则实数=34562.5344.514.已知向量和,则的最小值为15.如图,用三类不同的元件连接成一个系统,当正常工作且、至少有一个正常工作时,系统正常工作,已知正常工作的概率依次为、、,则系统正常工作的概率为16.数列的通项公式为,若是单调递增数列,则实数的取值范围是三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.)(12分)已知函数是偶函数;相邻两个零点间距离为.(1)求的单调递增区间;(2)已知为锐角三角形,角对边分别为,若,,,求18.(12分)某化肥厂甲、乙车间包装肥料,在自动包装传递带上每隔30min抽取一包产品,称其重量,分别记录抽查数据如下:甲:102,101,99,98,103,98,99乙:98,100,99,102,101,97,103(1)这种抽样方法是哪一种?(2)将这两组数据用茎叶图表示;(3)根据两组数据,获得样本的数字特征,对两个车间产品重量进行评价.(12分)如图,三棱柱中,底面,,,为中点.求证:平面平面。求二面角的余弦值。CABDC1B1A120.已知椭圆的中心为坐标原点,焦点在轴上,斜率为1且过椭圆右焦点的直线交椭圆于两点,与共线,(1)求椭圆的离心率;(2)设(异于)为椭圆上一点,且,求的值.21.已知:(1)若在区间上是减函数,求的取值范围;(2)设,判断根的个数,并说明理由。22.(本小题满分10分)选修4—1:几何证明选讲如图,已知与圆相切于点.经过点的割线交圆于点、,的平分线交、于点、(1)证明:(2)若,求的值.AEDCBP23.选修4—4:坐标系与参数方程在直角坐标系中,直线的参数方程为(为参数),若以点为极点,、轴正半轴为极轴建立极坐标系,则曲线的极坐标方程为.(1)求曲线的直角坐标方程及直线的普通方程(2)将曲线上各点的横坐标缩短为原来的,再将所得的曲线想左平移1个单位,得到曲线,求曲线上的点到直线的距离的最大值.24.选修4—5:不等式选讲设函数(1)当时,解不等式(2)若对成立,求的取值范围E